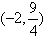Question

       设f(x)=x²–2ax+2,当x∈［–1,+∞)时，f(x)＞a恒成立，求a的取值范围 

Answer 1

a∈(–3,1

解析:

解法一:由f(x)＞a，在［–1,+∞)上恒成立

x²–2ax+2–a＞0在［–1,+∞)上恒成立.

考查函数g(x)=x²–2ax+2–a的图像在［–1,+∞］时位于x轴上方. 如图两种情况:

不等式的成立条件是:

(1)Δ=4a²–4(2–a)＜0a∈(–2,1)

(2)a∈(–3,–2，

综上所述a∈(–3,1).

解法二:由f(x)＞ax²+2＞a(2x+1)

令y₁=x²+2,y₂=a(2x+1),在同一坐标系中作出两个函数的图像.

如图满足条件的直线l位于l₁与l₂之间，而直线l₁、l₂对应的a值（即直线的斜率）分别为1，–3，故直线l对应的a∈(–3,1).