题目内容
从原点出发的某质点M,按向量a=(0,1)移动的概率为 ,按向量b=(0,2)移动的概率为
,按向量b=(0,2)移动的概率为 ,设M可到达点(0,n)的概率为Pn
,设M可到达点(0,n)的概率为Pn
(1)求P1和P2的值;(2)求证: =
= ;(3)求
;(3)求 的表达式。
的表达式。
 ,按向量b=(0,2)移动的概率为
,按向量b=(0,2)移动的概率为 ,设M可到达点(0,n)的概率为Pn
,设M可到达点(0,n)的概率为Pn(1)求P1和P2的值;(2)求证:
 =
= ;(3)求
;(3)求 的表达式。
的表达式。(1)P1= ,P2=
,P2= ; (2)证明见解析;(3)
; (2)证明见解析;(3)
 (-
(- )n
)n
 ,P2=
,P2= ; (2)证明见解析;(3)
; (2)证明见解析;(3)
 (-
(- )n
)n(1)P1= ,P2=(
,P2=( )2+
)2+ =
=
(2)证明:M到达点(0,n+2)有两种情况:①从点(0,n+1)按向量a=(0,1)移动;②从点(0,n)按向量b=(0,2)移动.
∴ +
+ ∴
∴ =
=
(3)数列{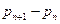 }是以P2-P1为首项,-
}是以P2-P1为首项,- 为公比的等比数列.
为公比的等比数列.
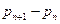 = (P2-P1)(-
= (P2-P1)(- )n-1=
)n-1= (-
(- )n-1=(-
)n-1=(- )n+1,
)n+1,
∴ =(-
=(- )n,
)n,
又∵ =(
=( )+(
)+(
 )+…+(P2-P1)
)+…+(P2-P1)
=(- )n+(-
)n+(- )n-1+…+(-
)n-1+…+(- )2=(
)2=(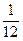 )[1- (-
)[1- (- )n-1]
)n-1]
∴ +(
+(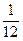 )[1- (-
)[1- (- )n-1]=
)n-1]= 
 (-
(- )n
)n
 ,P2=(
,P2=( )2+
)2+ =
=
(2)证明:M到达点(0,n+2)有两种情况:①从点(0,n+1)按向量a=(0,1)移动;②从点(0,n)按向量b=(0,2)移动.
∴
 +
+ ∴
∴ =
=
(3)数列{
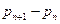 }是以P2-P1为首项,-
}是以P2-P1为首项,- 为公比的等比数列.
为公比的等比数列. 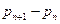 = (P2-P1)(-
= (P2-P1)(- )n-1=
)n-1= (-
(- )n-1=(-
)n-1=(- )n+1,
)n+1,∴
 =(-
=(- )n,
)n,又∵
 =(
=( )+(
)+(
 )+…+(P2-P1)
)+…+(P2-P1)=(-
 )n+(-
)n+(- )n-1+…+(-
)n-1+…+(- )2=(
)2=(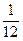 )[1- (-
)[1- (- )n-1]
)n-1]∴
 +(
+(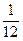 )[1- (-
)[1- (- )n-1]=
)n-1]= 
 (-
(- )n
)n
练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 ,则A、B同时发生的概率为( )
,则A、B同时发生的概率为( ) B.
B. C.
C. D. 0
D. 0