题目内容
已知中心在原点,焦点在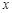 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为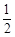 ,且经过点
,且经过点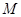
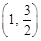 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)是否存过点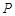 (2,1)的直线
(2,1)的直线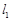 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点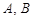 ,满足
,满足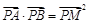 ?若存在,求出直线
?若存在,求出直线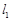 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
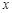 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为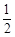 ,且经过点
,且经过点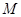
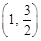 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)是否存过点
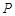 (2,1)的直线
(2,1)的直线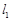 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点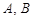 ,满足
,满足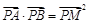 ?若存在,求出直线
?若存在,求出直线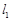 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.⑴ . ⑵y=1/2x
. ⑵y=1/2x
 . ⑵y=1/2x
. ⑵y=1/2x第一问利用设椭圆 的方程为
的方程为 ,由题意得
,由题意得
解得
第二问若存在直线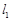 满足条件的方程为
满足条件的方程为 ,代入椭圆
,代入椭圆 的方程得
的方程得
 .
.
因为直线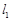 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点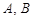 ,设
,设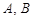 两点的坐标分别为
两点的坐标分别为 ,
,
所以
所以 .解得。
.解得。
解:⑴设椭圆 的方程为
的方程为 ,由题意得
,由题意得
解得 ,故椭圆
,故椭圆 的方程为
的方程为 .……………………4分
.……………………4分
⑵若存在直线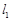 满足条件的方程为
满足条件的方程为 ,代入椭圆
,代入椭圆 的方程得
的方程得
 .
.
因为直线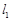 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点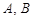 ,设
,设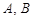 两点的坐标分别为
两点的坐标分别为 ,
,
所以
所以 .
.
又 ,
,
因为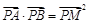 ,即
,即 ,
,
所以
 .
.
即 .
.
所以 ,解得
,解得 .
.
因为A,B为不同的两点,所以k=1/2.
于是存在直线L1满足条件,其方程为y=1/2x
 的方程为
的方程为 ,由题意得
,由题意得
解得

第二问若存在直线
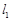 满足条件的方程为
满足条件的方程为 ,代入椭圆
,代入椭圆 的方程得
的方程得 .
.因为直线
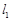 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点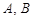 ,设
,设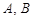 两点的坐标分别为
两点的坐标分别为 ,
,所以

所以
 .解得。
.解得。解:⑴设椭圆
 的方程为
的方程为 ,由题意得
,由题意得
解得
 ,故椭圆
,故椭圆 的方程为
的方程为 .……………………4分
.……………………4分⑵若存在直线
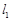 满足条件的方程为
满足条件的方程为 ,代入椭圆
,代入椭圆 的方程得
的方程得 .
.因为直线
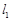 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点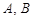 ,设
,设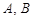 两点的坐标分别为
两点的坐标分别为 ,
,所以

所以
 .
.又
 ,
,因为
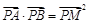 ,即
,即 ,
,所以

 .
.即
 .
.所以
 ,解得
,解得 .
.因为A,B为不同的两点,所以k=1/2.
于是存在直线L1满足条件,其方程为y=1/2x

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
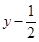 )2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.
)2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.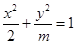 的离心率为
的离心率为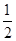 ,则m= ( )
,则m= ( ) 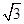
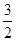
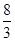
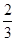
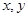 的方程
的方程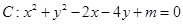 .
.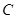 表示圆,求实数
表示圆,求实数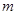 的取值范围 ;
的取值范围 ;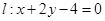 相交于
相交于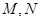 两点,且
两点,且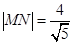 ,求
,求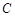 上动点
上动点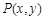 到定点
到定点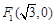 与定直线
与定直线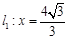 的距离之比为常数
的距离之比为常数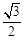 .
.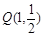 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点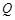 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程;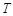 为圆心作圆
为圆心作圆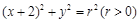 ,设圆
,设圆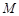 与点
与点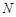 ,求
,求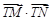 的最小值,并求此时圆
的最小值,并求此时圆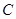 :
: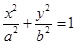
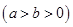 ,称圆心在坐标原点
,称圆心在坐标原点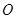 ,半径为
,半径为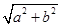 的圆是椭圆
的圆是椭圆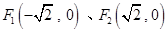 ,椭圆
,椭圆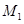 满足
满足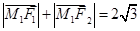 .
.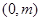
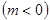 作直线
作直线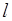 ,使得直线
,使得直线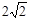 .求出
.求出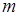 的值.
的值.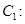
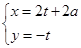 (
(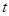 为参数),曲线
为参数),曲线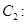
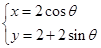 (
(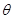 为参数).若曲线
为参数).若曲线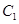 、
、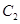 有公共点,则实数
有公共点,则实数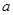 的取值范围_____.
的取值范围_____.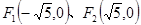 ,直线PF1和PF2相交于点P,且它们的斜率之积为定值
,直线PF1和PF2相交于点P,且它们的斜率之积为定值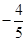 ;
;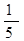 ),N为抛物线C2:
),N为抛物线C2: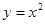 上的一动点,过点N作抛物线C2的切线交曲线C1于P、Q两点,求
上的一动点,过点N作抛物线C2的切线交曲线C1于P、Q两点,求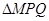 面积的最大值.
面积的最大值. O方程为
O方程为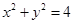 ,点P在圆上,点D在x轴上,点M在DP延长线上,
,点P在圆上,点D在x轴上,点M在DP延长线上,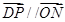 .且
.且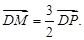
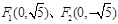 ,若过F1的直线交(I)中曲线C于A、B两点,求
,若过F1的直线交(I)中曲线C于A、B两点,求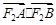 的取值范围.
的取值范围.