题目内容
直线l与直线2x+3y-17=0平行,且和两坐标轴围成的三角形面积为12.求直线l的方程.
分析:设直线l的方程为2x+3y+m=0(m≠0),则直线l与两坐标轴的交点 坐标,代入三角形的面积公式进行运算,求出参数m,即可得到直线方程.
解答:解:由题意可设直线l的方程为:2x+3y+m=0,
则可求直线l在x轴上的截距为-
,在y轴上的截距为-
,
继而由题意有:
×|-
||-
|=12?m=±12,
所以直线l的方程为:2x+3y+12=0或2x+3y-12=0.
则可求直线l在x轴上的截距为-
| m |
| 2 |
| m |
| 3 |
继而由题意有:
| 1 |
| 2 |
| m |
| 2 |
| m |
| 3 |
所以直线l的方程为:2x+3y+12=0或2x+3y-12=0.
点评:本题考查用待定系数法求直线的方程,两直线平行的性质,以及利用直线的截距求三角形的面积.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 ,则直线l的斜率为
,则直线l的斜率为 

 ,则直线l的斜率为
,则直线l的斜率为 

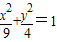 及点M(1,1).
及点M(1,1).