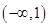题目内容
已知函数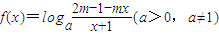 是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).(1)求实数m的值,并写出区间D;
(2)若底数a满足0<a<1,试判断函数y=f(x)在定义域D内的单调性,并说明理由;
(3)当x∈A=[a,b)(A⊆D,a是底数)时,函数值组成的集合为[1,+∞),求实数a、b的值.
【答案】分析:(1)根据奇函数的性质,得到任意x∈D,有f(x)+f(-x)=0,即可得到(m2-1)x2-(2m-1)2+1=0在D内恒成立,即得到 即可得到m,写出区间D;
即可得到m,写出区间D;
(2)令 ,在在D=(-1,1)上是随x增大而减小,根据复合函数的单调性即可判断;
,在在D=(-1,1)上是随x增大而减小,根据复合函数的单调性即可判断;
(3)根据A⊆D,结合(2)知函数 上是增函数,得到
上是增函数,得到 得到a,在根据若b<1,则f(x)在A上的函数值组成的集合为
得到a,在根据若b<1,则f(x)在A上的函数值组成的集合为 ,不满足函数值组成的集合是[1,+∞)的要求,得到b.
,不满足函数值组成的集合是[1,+∞)的要求,得到b.
解答:解(1)∵y=f(x)是奇函数,
∴对任意x∈D,有f(x)+f(-x)=0,即 .
.
化简此式,得(m2-1)x2-(2m-1)2+1=0.又此方程有无穷多解(D是区间),
必有 ,解得m=1.
,解得m=1.
∴ .
.
(2)当0<a<1时,函数 上是单调增函数.
上是单调增函数.
理由:令 .
.
易知1+x在D=(-1,1)上是随x增大而增大, 在D=(-1,1)上是随x增大而减小,
在D=(-1,1)上是随x增大而减小,
故 在D=(-1,1)上是随x增大而减小
在D=(-1,1)上是随x增大而减小
于是,当0<a<1时,函数 上是单调增函数.
上是单调增函数.
(3)∵x∈A=[a,b)(A⊆D,a是底数)
∴0<a<1,a<b≤1.
∴由(2)知,函数 上是增函数,即
上是增函数,即 ,
,
解得 .
.
若b<1,则f(x)在A上的函数值组成的集合为 ,不满足函数值组成的集合是[1,+∞)的要求,
,不满足函数值组成的集合是[1,+∞)的要求,
∴必有b=1.
因此,所求实数a、b的值是 .
.
点评:本题从恒等式出发得到m,另外复合函数的单调性的判断关键在于分离出单个函数,属于中档题.
 即可得到m,写出区间D;
即可得到m,写出区间D;(2)令
 ,在在D=(-1,1)上是随x增大而减小,根据复合函数的单调性即可判断;
,在在D=(-1,1)上是随x增大而减小,根据复合函数的单调性即可判断;(3)根据A⊆D,结合(2)知函数
 上是增函数,得到
上是增函数,得到 得到a,在根据若b<1,则f(x)在A上的函数值组成的集合为
得到a,在根据若b<1,则f(x)在A上的函数值组成的集合为 ,不满足函数值组成的集合是[1,+∞)的要求,得到b.
,不满足函数值组成的集合是[1,+∞)的要求,得到b.解答:解(1)∵y=f(x)是奇函数,
∴对任意x∈D,有f(x)+f(-x)=0,即
 .
.化简此式,得(m2-1)x2-(2m-1)2+1=0.又此方程有无穷多解(D是区间),
必有
 ,解得m=1.
,解得m=1.∴
 .
.(2)当0<a<1时,函数
 上是单调增函数.
上是单调增函数.理由:令
 .
.易知1+x在D=(-1,1)上是随x增大而增大,
 在D=(-1,1)上是随x增大而减小,
在D=(-1,1)上是随x增大而减小,故
 在D=(-1,1)上是随x增大而减小
在D=(-1,1)上是随x增大而减小于是,当0<a<1时,函数
 上是单调增函数.
上是单调增函数.(3)∵x∈A=[a,b)(A⊆D,a是底数)
∴0<a<1,a<b≤1.
∴由(2)知,函数
 上是增函数,即
上是增函数,即 ,
,解得
 .
.若b<1,则f(x)在A上的函数值组成的集合为
 ,不满足函数值组成的集合是[1,+∞)的要求,
,不满足函数值组成的集合是[1,+∞)的要求,∴必有b=1.
因此,所求实数a、b的值是
 .
.点评:本题从恒等式出发得到m,另外复合函数的单调性的判断关键在于分离出单个函数,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式; .
.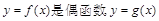 是奇函数,它们的定域
是奇函数,它们的定域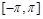 ,且它们在
,且它们在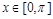 上的图象如图所示,则不等式
上的图象如图所示,则不等式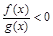 的解集是 .
的解集是 .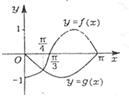
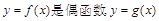 是奇函数,它们的定域
是奇函数,它们的定域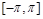 ,且它们在
,且它们在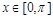 上的图象如图所示,则不等式
上的图象如图所示,则不等式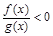 的解集是 .
的解集是 .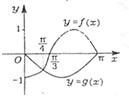
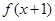 是定义在R上的奇函数,若对于任意给
是定义在R上的奇函数,若对于任意给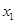 、
、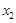 ,不等式
,不等式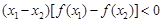
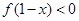 的解集为( ※ )
的解集为( ※ )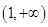 B.
B.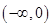 C.
C.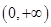 D.
D.