题目内容
 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为2的等边三角形,D为AB边中点,且CC1=2AB.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为2的等边三角形,D为AB边中点,且CC1=2AB.(1)求证:平面C1CD⊥平面ABC;
(2)求二面角C-AB-C1的平面角的正弦值;
(3)求三棱锥D-CBB1的体积.
分析:(1)由已知中CC1⊥平面ABC,由面面垂直的判定定理,即可得到平面C1CD⊥平面ABC;
(2)由已知中等边三角形ABC中,D为AB边中点,则CD⊥AB,又由CC1⊥平面ABC,可得AB⊥C1D,故∠C1DC为二面角C-AB-C1的平面角,解Rt△C1DC,即可得到二面角C-AB-C1的平面角的正弦值;
(3)由已知中CC1⊥平面ABC,CC1∥BB1,BB1⊥平面ABC,求出△ABC的面积,代入棱锥的体积公式,即可得到三棱锥D-CBB1的体积.
(2)由已知中等边三角形ABC中,D为AB边中点,则CD⊥AB,又由CC1⊥平面ABC,可得AB⊥C1D,故∠C1DC为二面角C-AB-C1的平面角,解Rt△C1DC,即可得到二面角C-AB-C1的平面角的正弦值;
(3)由已知中CC1⊥平面ABC,CC1∥BB1,BB1⊥平面ABC,求出△ABC的面积,代入棱锥的体积公式,即可得到三棱锥D-CBB1的体积.
解答:解:(1)证明:∵CC1⊥平面ABC,CC1?平面C1CD
∴平面C1CD⊥平面ABC
(2)在等边三角形ABC中,D为AB边中点
∴CD⊥AB
∵CC1⊥平面ABC,
AB?平面ABC
∴CC1⊥AB又
∵CC1∩CD=C
∴AB⊥平面C1CD,
又∵C1D?平面C1CD
∴AB⊥C1D
所以,∠C1DC为二面角C-AB-C1的平面角
在Rt△C1DC中,CC1⊥CD,CC1=AB=4,CD=
=
C1D=
=
∴sin∠C1DC=
=
=
所以,二面角C-AB-C1的平面角的正弦值为
;
(3)∵CC1⊥平面ABC
CC1∥BB1
∴BB1⊥平面ABC
∴VD-CBB1=VB1-BCD=
•S△BCD•BB1=
•(
×1×
)•4=
所以,三棱锥D-CBB1的体积为
∴平面C1CD⊥平面ABC
(2)在等边三角形ABC中,D为AB边中点
∴CD⊥AB
∵CC1⊥平面ABC,
AB?平面ABC
∴CC1⊥AB又
∵CC1∩CD=C
∴AB⊥平面C1CD,
又∵C1D?平面C1CD
∴AB⊥C1D
所以,∠C1DC为二面角C-AB-C1的平面角
在Rt△C1DC中,CC1⊥CD,CC1=AB=4,CD=
| 22-12 |
| 3 |
| CC12+CD2 |
| 19 |
∴sin∠C1DC=
| CC1 |
| C1D |
| 4 | ||
|
4
| ||
| 19 |
所以,二面角C-AB-C1的平面角的正弦值为
4
| ||
| 19 |
(3)∵CC1⊥平面ABC
CC1∥BB1
∴BB1⊥平面ABC
∴VD-CBB1=VB1-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
所以,三棱锥D-CBB1的体积为
2
| ||
| 3 |
点评:本题考查的知识点是二面角的平面角及求法,棱锥的体积公式,平面与平面垂直的判定,其中(1)的关键是由线面垂直得到面面垂直,(2)的关键是证明得∠C1DC为二面角C-AB-C1的平面角,(3)的关键是证得BB1⊥平面ABC.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=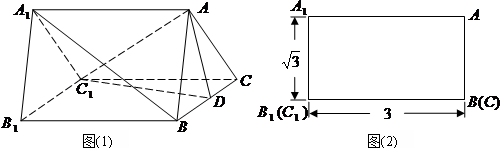
 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,
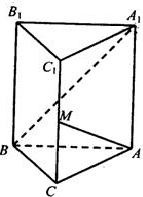
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1, 如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.
如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.