Question

【题目】已知函数f（x）=x2+ax+3．

（1）当x∈R时，f（x）≥a恒成立，求a的取值范围．

（2）当a∈[4，6]时，f（x）≥0恒成立，求x的取值范围．

Answer 1

【答案】（1）-6≤a≤2; （2）{x|x≤-3-或x≥-3+}

【解析】

（1）f（x）≥a恒成立，x2+ax+3-a≥0对任意x∈R恒成立，根据判别式进而求解；

（2）设g（a）=x2+ax+3，转化成关于a的一次函数，进而求解．

解：（1）∵函数f（x）=x2+ax+3，当x∈R时，f（x）≥a恒成立，

∴x2+ax+3-a≥0对任意x∈R恒成立，

∴△=a2-4（3-a）≤0，

化简得a2+4a-12≤0，

解得：-6≤a≤2；

（2）设g（a）=x2+ax+3，

则由题可得：当a∈[4，6]时，恒有g（a）≥0，

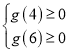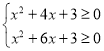∴ 即 解得，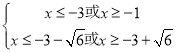

即x≤-3-或x≥-3+，

∴x的取值范围是{x|x≤-3-或x≥-3+}．