题目内容
下列结论中，错误的是
- A.x，y均为正数，则
- B.a为正数，则
- C.lgx+
其中x＞1 - D.
B
分析：利用基本不等式对A，B，C，D四个选项逐一判断即可．
解答：对于A，x，y均为正数，则
+
≥2（当且仅当x=y=1时取等号），故A正确；
对于B，a为正数，（
+
）（a+
）=
+
+2+
≥
，（当且仅当a=1时取等号），故B错误；
对于C，当x＞1时，lgx+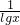
≥2（当且仅当x=10时取等号），故C正确；
对于D，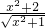
=
+
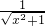≥2（当且仅当x=0时取等号），故D正确；
故选B．
点评：本题考查基本不等式，对基本不等式中“一正，二定，三等”三条件缺一不可的理解与应用是关键，属于中档题．
分析：利用基本不等式对A，B，C，D四个选项逐一判断即可．
解答：对于A，x，y均为正数，则
+≥2（当且仅当x=y=1时取等号），故A正确；对于B，a为正数，（
+）（a+）=++2+≥，（当且仅当a=1时取等号），故B错误；对于C，当x＞1时，lgx+
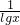≥2（当且仅当x=10时取等号），故C正确；对于D，
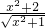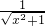=+≥2（当且仅当x=0时取等号），故D正确；故选B．
点评：本题考查基本不等式，对基本不等式中“一正，二定，三等”三条件缺一不可的理解与应用是关键，属于中档题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
已知定义在[1，8]上的函数f(x)=
．则下列结论中，错误的是（ ）
|
| A、f（3）=2 |
| B、函数f（x）的值域为[0，4] |
| C、对任意的x∈[1，8]，不等式xf（x）≤6恒成立 |
| D、将函数f（x）的极值由大到小排列得到数列{an}，n∈N*，则{an}为等比数列 |
已知定义在[1，8]上的函数 f(x)=
则下列结论中，错误的是（ ）
|
| A、f（6）=1 |
| B、函数f（x）的值域为[0，4] |
| C、将函数f（x）的极值由大到小排列得到数列{an}，n∈N*，则{an}为等比数列 |
| D、对任意的x∈[1，8]，不等式xf（x）≤6恒成立 |
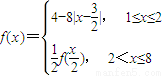则下列结论中，错误的是（ ）
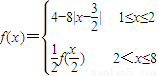．则下列结论中，错误的是（ ）