题目内容
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点在椭圆
的对称点在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
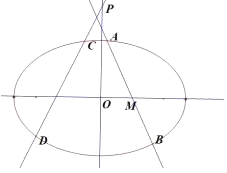
(2)如图,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两个不同的点
交于两个不同的点![]() (点
(点![]() 在点
在点![]() 的上方),试求
的上方),试求![]() 面积的最大值;
面积的最大值;
(3)若直线![]() 经过点
经过点![]() ,且与椭圆
,且与椭圆![]() 交于两个不同的点
交于两个不同的点![]() ,是否存在直线
,是否存在直线![]() (其中
(其中![]() ),使得
),使得![]() 到直线
到直线![]() 的距离
的距离![]() 满足
满足![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)1;(3)存在,4.
;(2)1;(3)存在,4.
【解析】
(1)根据椭圆的焦距求出c,由P(0,2)关于直线y=﹣x的对称点在椭圆Γ上可得a=2,即可求出b2,可得椭圆方程;
(2)设过点P(0,2)的直线方程为y=mx+2,代入椭圆方程,运用韦达定理,弦长公式和点到直线的距离,表示出三角形的面积,再根据函数的性质即可求出最值;
(3)设直线l的方程为y=k(x﹣1),代入椭圆方程,运用韦达定理,假设存在这样的直线l0,运用点到直线的距离公式和两点的距离公式,可得![]() ,化简整理代入,即可判断.
,化简整理代入,即可判断.
(1)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,
,
因为![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,又
,又![]() ,故
,故![]() ,
,
则![]() .所以,椭圆
.所以,椭圆![]() 的方程为
的方程为![]() .
.
(2)由题意,直线![]() 的斜率存在,设
的斜率存在,设![]() 的方程为
的方程为![]() ,
,
由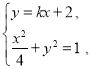 得
得![]() ,
,
由△![]() ,得
,得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,且
,且![]() ,
,
![]() ,
,
所以,![]()
![]() .
.
令![]() ,则
,则![]() ,所以,
,所以,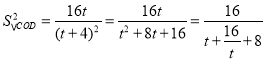 ,
,
因为![]() (当且仅当
(当且仅当![]() 时等号成立),此时
时等号成立),此时![]() .
.
所以,当且仅当![]() ,即
,即![]() 时,△
时,△![]() 的面积取最大值
的面积取最大值![]() .
.
(3)当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 的方程为
的方程为![]() ,此时
,此时![]() ,
,![]() ,
,
等式![]() 成立;
成立;
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
由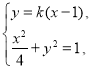 得
得![]() ,
,
span>设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
由题意,![]() 与
与![]() 一个小于
一个小于![]() ,另一个大于
,另一个大于![]() ,不妨设
,不妨设![]() ,
,
则![]()
![]()
![]()
![]()
![]() ,
,
所以,![]() ,
,
即![]() ,解得
,解得![]() .
.
综上,存在满足条件的直线![]() ,使得
,使得![]() 恒成立.
恒成立.

练习册系列答案
相关题目