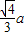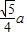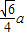题目内容
平面几何中有命题“正三角形内任意一点到三边的距离之和等于定值，大小为边长的
倍”，请你写出此命题在立体几何中类似的真命题________．
正四面体内任意一点到四个面的距离之和是一个定值，大小为棱长的
倍．
分析：由题意平面几何中有命题“正三角形内任意一点到三边的距离之和等于定值，大小为边长的倍，类似可以写此命题在立体几何中类似的真命题 正四面体内任意一点到四个面的距离之和是一个定值，大小为棱长的
倍．
解答：设正三角形的边长为a，
∵正三角形内任意一点到三边的距离之和等于定值，大小为边长的倍”，
∴正三角形的中心0到边长的距离为：
×a=
a，
∵正四面体内的底面也是正三角形，
∴正四面体侧面的高为：h=
=
，
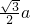∴正四面体顶点到底边的距离l=
=
，
∵四面体内任意一点到四个面的距离之和就是正四面体顶点到底边的距离l，
∴正四面体内任意一点到四个面的距离之和是一个定值，大小为棱长的倍．
点评：此题主要考查命题的归纳和类比，利用平面几何的性质，类比到立体几何上，题比较新颖，是一道好题．
倍．分析：由题意平面几何中有命题“正三角形内任意一点到三边的距离之和等于定值，大小为边长的
倍，类似可以写此命题在立体几何中类似的真命题 正四面体内任意一点到四个面的距离之和是一个定值，大小为棱长的倍．解答：设正三角形的边长为a，
∵正三角形内任意一点到三边的距离之和等于定值，大小为边长的
倍”，∴正三角形的中心0到边长的距离为：
×a=a，∵正四面体内的底面也是正三角形，
∴正四面体侧面的高为：h=
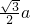=，∴正四面体顶点到底边的距离l=
=，∵四面体内任意一点到四个面的距离之和就是正四面体顶点到底边的距离l，
∴正四面体内任意一点到四个面的距离之和是一个定值，大小为棱长的
倍．点评：此题主要考查命题的归纳和类比，利用平面几何的性质，类比到立体几何上，题比较新颖，是一道好题．
练习册系列答案
相关题目
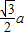，类比上述命题，棱长为a的正四面体内任一点到四个面的距离之和为（ ）
