题目内容
已知命题p:方程a2x2+ax-2=0在[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0,若命题“p或q”是假命题,求a的取值范围.
解析:由a2x2+ax-2=0,
得(ax+2)(ax-1)=0,
显然a≠0,∴x=-![]() 或x=
或x=![]() .
.
∵x∈[-1,1],故|![]() |≤1或|
|≤1或|![]() |≤1,
|≤1,
∴|a|≥1.
“只有一个实数满足x2+2ax+2a≤0”.即抛物线y=x2+2ax+2a与x轴只有一个交点,∴Δ=4a2-8a=0.∴a=0或2,
∴命题“p或q为真命题”时“|a|≥1或a=0”.
∵命题“p或Q”为假命题,
∴a的取值范围为{a|-1<a<0或0<a<1}.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
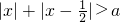 恒成立;若P或q为真,P且q为假,求实数a的取值范围.
恒成立;若P或q为真,P且q为假,求实数a的取值范围. 恒成立;若P或q为真,P且q为假,求实数a的取值范围.
恒成立;若P或q为真,P且q为假,求实数a的取值范围.