题目内容
已知函数 ,下列命题正确的是 。(写出所有正确命题的序号)
,下列命题正确的是 。(写出所有正确命题的序号)
①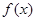 是奇函数; ②对定义域内任意x,
是奇函数; ②对定义域内任意x,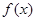 <1恒成立;
<1恒成立;
③当 时,
时,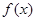 取得极小值; ④
取得极小值; ④ ; ⑤当x>0时,若方程|
; ⑤当x>0时,若方程|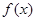 |=k有且仅有两个不同的实数解
|=k有且仅有两个不同的实数解 ·cos
·cos =-sin
=-sin 。
。
②④⑤.
解析试题分析: 的定义域为{x|x
的定义域为{x|x 0}.因为f(-x)=f(x),所以其为偶函数;①错;
0}.因为f(-x)=f(x),所以其为偶函数;①错;
因为|sinx| 1,且当0<x<
1,且当0<x< 时,sinx<x,所以
时,sinx<x,所以 <1成立; ②对;
<1成立; ②对;
由于函数的导数 ,
,
x= 时,
时,
 0,所以③错;
0,所以③错;
由x∈( ,
, )时,xcosx-sinx<0,即f'(x)<0,知函数在区间(
)时,xcosx-sinx<0,即f'(x)<0,知函数在区间( ,
, )为减函数,所以④
)为减函数,所以④ 对;
对;
⑤当x>0时,若方程|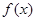 |=k有且仅有两个不同的实数解
|=k有且仅有两个不同的实数解 ,由于(0,π)上f(x)>0,(π,2π)上f(x)<0,所以
,由于(0,π)上f(x)>0,(π,2π)上f(x)<0,所以 (导数为零),
(导数为零),
结合图象知 ·cos
·cos =-sin
=-sin 。
。
综上知,答案为②④⑤.
考点:本题主要考查三角函数的图象和性质,利用导数研究函数的单调性、求极值,数形结合思想。
点评:中档题,本题综合性较强,解答过程中,时而运用函数图象,时而运用导数知识,体现应用数学知识的灵活性。

练习册系列答案
相关题目
下列四个命题中,正确的是( )
| A、对于命题p:?x∈R,使得x2+x+1<0,则-p:?x∈R,均有x2+x+1>0 | ||
| B、函数f(x)=e-x-ex切线斜率的最大值是2 | ||
| C、已知ξ服从正态分布N(0,ρ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.2; | ||
D、已知函数f(a)=∫0asinxdx,则f[f(
|
 给出下列四个命题:
给出下列四个命题: