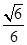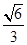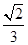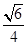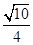题目内容
三棱锥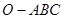 中,
中, 两两垂直且相等,点
两两垂直且相等,点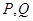 分别是线段
分别是线段 和
和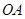 上移动,且满足
上移动,且满足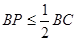 ,
,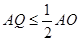 ,则
,则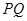 和
和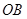 所成角余弦值的取值范围是( )
所成角余弦值的取值范围是( )
A.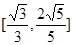 | B. | C.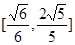 | D.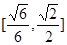 |
C.
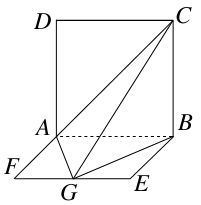
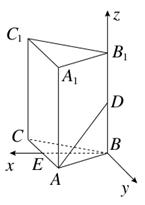
解析试题分析:以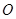 为原点,分别
为原点,分别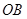 ,
, ,
,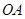 为
为 ,
,  ,
,  轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
不妨设 ,
, ,
,  ,则由
,则由 ,
,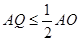 得出
得出 ,
, ,
, ,
, .于是向量
.于是向量 ,
, ,所以
,所以 ,
,
令 ,
, ,则
,则 .
.
因为对称轴为 ,所以
,所以 关于
关于 为递增函数,关于
为递增函数,关于 为递增函数.
为递增函数.
又因为 与
与 独立取值,所以
独立取值,所以 ,所以
,所以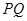 和
和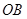 所成角余弦值的取值范围为
所成角余弦值的取值范围为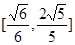 ,即为所求.
,即为所求.
考点:立体几何与空间向量.

练习册系列答案
相关题目
已知平面α内有一个点A(2,-1,2),α的一个法向量为n=(3,1,2),则下列点P中,在平面α内的是( )
| A.(1,-1,1) | B.(1,3,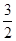 ) ) |
C.(1,-3,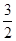 ) ) | D.(-1,3,-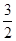 ) ) |
在空间直角坐标系中,点A(1,﹣1,1)与点B(﹣1,﹣1,﹣1)关于( )对称
| A.x轴 | B.y轴 | C.z轴 | D.原点 |
若直线l⊥平面α,直线l的方向向量为s,平面α的法向量为n,则下列结论正确的是( )
| A.s=(1,0,1),n=(1,0,-1) |
| B.s=(1,1,1),n=(1,1,-2) |
| C.s=(2,1,1),n=(-4,-2,-2) |
| D.s=(1,3,1),n=(2,0,-1) |
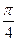 。
。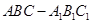 的底面
的底面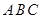 位于平行四边形
位于平行四边形 中,
中,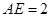 ,
,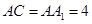 ,
, ,点
,点 为
为 中点.
中点.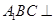 平面
平面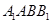 .
.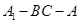 的大小为
的大小为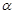 ,直线
,直线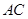 与平面
与平面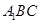 所成的角为
所成的角为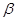 ,求
,求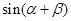 的值.
的值.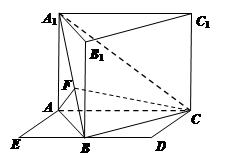

 ∠AEF=45°
∠AEF=45°
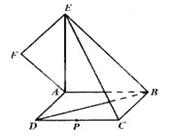
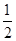 AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )