题目内容
某种商品原来定价为每件p元,每月将卖出n件.假若定价上涨x成(注:x成即 ,0<x≤10),每月卖出数量将减少y成,而销售金额变成原来的z倍.
,0<x≤10),每月卖出数量将减少y成,而销售金额变成原来的z倍.
(1)若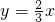 ,求使销售金额比原来有所增加时的x的取值范围;
,求使销售金额比原来有所增加时的x的取值范围;
(2)若y=ax,其中a是满足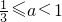 的常数,用a来表示当销售金额最大时x的值.
的常数,用a来表示当销售金额最大时x的值.
解:(1)该商品定价上涨x成时,上涨后的定价、每月卖出数量、每月售货金额分别是
p(1+ ),n(1-
),n(1-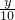 ),npz
),npz
因而有:npz=p(1+ )•n(1-
)•n(1-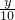 ),
),
∴z= ,
,
当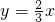 时
时
由z=
得0<x<5
(2)该商品定价上涨x成时,上涨后的定价、每月卖出数量、每月售货金额分别是
p(1+ ),n(1-
),n(1-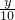 ),npz
),npz
因而有:npz=p(1+ )•n(1-
)•n(1-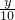 ),
),
∴z= ,在y=ax的条件下
,在y=ax的条件下
z= ,
,
∵ ,
,
∴10-ax>0
∴(10a+ax)(10-ax)≤ ,
,
当且仅当10a+ax=10-ax,即x= 时成立.
时成立.
即要使的销售金额最大,只要z值最大,这时应有x= .
.
分析:(1)定价上涨x成时,上涨后的定价、每月卖出数量、每月售货金额分别是p(1+ ),n(1-
),n(1-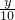 ),npz,写出要的算式,使得式子大于1,解出关于x的不等式,得到结果.
),npz,写出要的算式,使得式子大于1,解出关于x的不等式,得到结果.
(2)定价上涨x成时,上涨后的定价、每月卖出数量、每月售货金额分别是p(1+ ),n(1-
),n(1-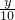 ),npz,写出要的算式,把所给的关系代入关系式,根据基本不等式得到结果,求出答案.
),npz,写出要的算式,把所给的关系代入关系式,根据基本不等式得到结果,求出答案.
点评:本题以实际问题为载体,主要考查了二次函数的应用,二次函数的最值,解一元二次方程等知识点,解此题的关键是把实际问题转化成数学问题,这是一道很好的题目.
p(1+
 ),n(1-
),n(1-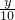 ),npz
),npz因而有:npz=p(1+
 )•n(1-
)•n(1-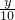 ),
),∴z=
 ,
,当
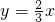 时
时由z=

得0<x<5
(2)该商品定价上涨x成时,上涨后的定价、每月卖出数量、每月售货金额分别是
p(1+
 ),n(1-
),n(1-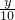 ),npz
),npz因而有:npz=p(1+
 )•n(1-
)•n(1-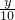 ),
),∴z=
 ,在y=ax的条件下
,在y=ax的条件下 z=
 ,
,∵
 ,
,∴10-ax>0
∴(10a+ax)(10-ax)≤
 ,
,当且仅当10a+ax=10-ax,即x=
 时成立.
时成立.即要使的销售金额最大,只要z值最大,这时应有x=
 .
.分析:(1)定价上涨x成时,上涨后的定价、每月卖出数量、每月售货金额分别是p(1+
 ),n(1-
),n(1-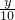 ),npz,写出要的算式,使得式子大于1,解出关于x的不等式,得到结果.
),npz,写出要的算式,使得式子大于1,解出关于x的不等式,得到结果.(2)定价上涨x成时,上涨后的定价、每月卖出数量、每月售货金额分别是p(1+
 ),n(1-
),n(1-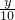 ),npz,写出要的算式,把所给的关系代入关系式,根据基本不等式得到结果,求出答案.
),npz,写出要的算式,把所给的关系代入关系式,根据基本不等式得到结果,求出答案.点评:本题以实际问题为载体,主要考查了二次函数的应用,二次函数的最值,解一元二次方程等知识点,解此题的关键是把实际问题转化成数学问题,这是一道很好的题目.

练习册系列答案
相关题目
 ”,0<x≤10),每月卖出的数量将减少y成,而销售金额变成原来的z倍,若y=
”,0<x≤10),每月卖出的数量将减少y成,而销售金额变成原来的z倍,若y= x,求使销售金额比原来有所增加的x的取值范围。
x,求使销售金额比原来有所增加的x的取值范围。