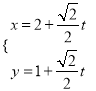题目内容
【题目】已知抛物线![]() 与二次曲线
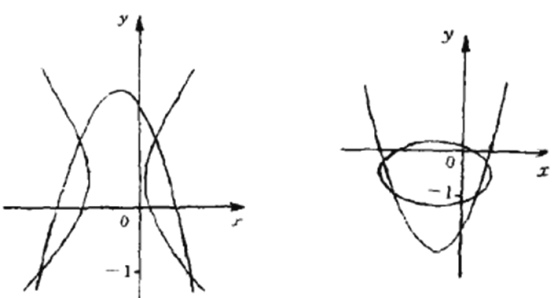
与二次曲线![]() 有4个不同的交点,由下面的草图可以看出,下面三个结论是成立的,请给出证明.
有4个不同的交点,由下面的草图可以看出,下面三个结论是成立的,请给出证明.
(1).两曲线的4个交点中,至少有两个交点位于![]() 轴的下方;
轴的下方;
(2).抛物线![]() 必与
必与![]() 轴有两个不同的交点,记为
轴有两个不同的交点,记为![]() ,
,![]() ,
,![]() ;
;
(3).两曲线的4个交点中,必存在一点![]() ,使
,使![]() .
.
注.对![]() 、
、![]() 、
、![]() 的不同取值会有无数个图形,此处仅就
的不同取值会有无数个图形,此处仅就![]() ,
,![]() 各给出一个示意图,同时也就限制“由图看出”的解答.
各给出一个示意图,同时也就限制“由图看出”的解答.
【答案】(1)见解析(2)见解析(3)见解析
【解析】
(1).联立方程组
![]() .
.
消去![]() ,得
,得![]()
解得![]() ,
,![]() .
.
则两曲线的4个交点中,至少有两个交点的纵坐标为负数(![]() 是小于0的,并且
是小于0的,并且![]() 也有可能小于0),这两点位于
也有可能小于0),这两点位于![]() 轴的下方.
轴的下方.
(2)由上证知,四个交点中有纵坐标为![]() 的,取其中一个为
的,取其中一个为![]() ,代入抛物线方程得
,代入抛物线方程得![]() . ①
. ①
两边乘以![]() 后,配方得
后,配方得
![]() .
.
则![]() .
.
这表明,二次方程
![]() ②
②
的判别式大于0,从而有两个不相等的实根,记为![]() ,
,![]()
![]() ,得抛物线与
,得抛物线与![]() 轴交于两点
轴交于两点![]() ,
,![]() .
.
(3)由![]() 、
、![]() 是方程②的两个根知
是方程②的两个根知
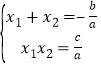 . ③
. ③
又由①有![]() .
.
把③代入,得![]() ,即
,即![]() .
.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目