题目内容
已知动圆过定点M(0,1),且与直线L:y=-1相切..(1)求动圆圆心C的轨迹的方程;
(2)设A、B是轨迹C上异于原点O的两个不同点,直线OA和OB的倾斜角分别
为α和β,当α,β变化且α+β=θ
 为定值时,证明:直线AB恒过定点,并求出该定点的坐标.
为定值时,证明:直线AB恒过定点,并求出该定点的坐标.
【答案】分析:(1)依据抛物线的定义即可得C的轨迹的方程;
(2)欲求证直线AB恒过定点,可先根据条件求出带参数θ的直线AB的方程,再结合θ为定值即可证得.
解答:解:(1)由抛物线定义知C的轨迹是抛物线,且p=2,
∴动圆圆心C的轨迹方程:x2=4y(6分)
(2)设点
则直线AB的方程为: ,
,
化简得: (9分)
(9分)
又因为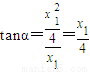 ,
,
由α+β=θ,得tanθ=
则 ,
,
所以 (12分)
(12分)
所以直线AB方程为
即
所以直线AB过定点 .(15分)
.(15分)
点评:定义法:运用解析几何中一些常用定义(例如圆锥曲线的定义),可从曲线定义出发直接写出轨迹方程,或从曲线定义出发建立关系式,从而求出轨迹方程.
(2)欲求证直线AB恒过定点,可先根据条件求出带参数θ的直线AB的方程,再结合θ为定值即可证得.
解答:解:(1)由抛物线定义知C的轨迹是抛物线,且p=2,
∴动圆圆心C的轨迹方程:x2=4y(6分)
(2)设点

则直线AB的方程为:
 ,
,化简得:
 (9分)
(9分)又因为
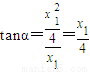 ,
,
由α+β=θ,得tanθ=

则
 ,
,所以
 (12分)
(12分)所以直线AB方程为

即

所以直线AB过定点
 .(15分)
.(15分)点评:定义法:运用解析几何中一些常用定义(例如圆锥曲线的定义),可从曲线定义出发直接写出轨迹方程,或从曲线定义出发建立关系式,从而求出轨迹方程.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 相切,点C在
相切,点C在 上.
上. 的直线与曲线交于A、B两点.问直线
的直线与曲线交于A、B两点.问直线 是以
是以 为直角的直角三角形?如果存在,求出点C的坐标;若不能,请说明理由.
为直角的直角三角形?如果存在,求出点C的坐标;若不能,请说明理由.