Question

如图，在正方体ABCD-A₁B₁C₁D₁中，|

AB

|=1，

A1P

=λ

A1C

(0＜λ＜1)．
（1）若λ=

1

2

，求直线PB与PD所成角的正弦值；
（2）是否存在实数λ，使得直线A₁C⊥平面PBD？并说明理由．

Answer 1

分析：（1）建立空间直角坐标系，用坐标表示点，从而可得向量的坐标，利用向量的夹角公式，即可求得直线PB与PD所成角的正弦值；
（2）假设存在符合条件的实数λ，验证A₁C⊥BD．要使A₁C⊥平面PBD，只需BP⊥A₁C，利用

A1C

•

BP

=0，即可求得实数λ．

解答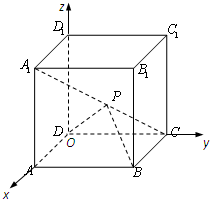：解：（1）如图，分别以DA，DC，D D₁为x轴，y轴，z轴建立空间直角坐标系O-xyz，则A（1，0，0），B（1，1，0），C（0，1，0），D（0，0，0），A₁（1，0，1），B₁（1，1，1），C₁（0，1，1），D₁（0，0，1），
由λ=

1

2

得P(

1

2

，

1

2

，

1

2

)，
所以

PB

=(

1

2

，

1

2

，-

1

2

)，

PD

=(-

1

2

，-

1

2

，-

1

2

)，
所以cos?

PB

•

PD

＞=

- 1 4 - 1 4 + 1 4

3 2 • 3 2

=-

1

3

，
所以，直线PB与PD所成角的正弦值为

2 2

3

．（5分）
（2）假设存在符合条件的实数λ，
因为

A1C

=(-1，1，-1)，

BD

=(-1，-1，0)，所以

A1C

•

BD

=0，故A₁C⊥BD．
要使A₁C⊥平面PBD，只需BP⊥A₁C，由

A1P

=λ

A1C

=λ(-1，1，-1)得P（1-λ，λ，1-λ），
此时

BP

=(-λ，λ-1，1-λ)，由

A1C

•

BP

=0得λ=

2

3

．（10分）

点评：本题主要考查空间向量的应用，考查线线角，考查线面垂直，考查运算求解能力，属于中档题．