题目内容
已知数列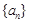 的前
的前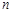 项和为
项和为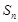 ,且
,且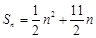 。数列
。数列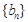 满足
满足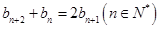 ,
,
且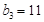 ,
,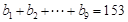 。
。
(1)求数列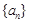 ,
,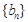 的通项公式;
的通项公式;
(2)设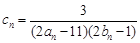 ,数列
,数列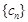 的前
的前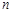 项和为
项和为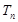 ,求使不等式
,求使不等式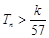 对一切
对一切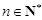 都成立的最大正整数
都成立的最大正整数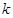 的值;
的值;
(3)设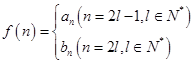 ,是否存在
,是否存在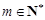 ,使得
,使得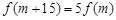 成立?若存在,求出
成立?若存在,求出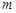 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
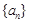 的前
的前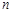 项和为
项和为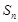 ,且
,且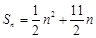 。数列
。数列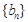 满足
满足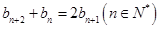 ,
,且
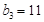 ,
,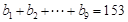 。
。(1)求数列
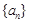 ,
,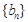 的通项公式;
的通项公式;(2)设
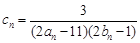 ,数列
,数列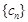 的前
的前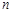 项和为
项和为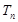 ,求使不等式
,求使不等式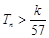 对一切
对一切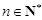 都成立的最大正整数
都成立的最大正整数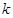 的值;
的值;(3)设
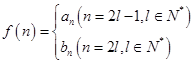 ,是否存在
,是否存在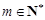 ,使得
,使得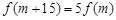 成立?若存在,求出
成立?若存在,求出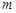 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。(1) 。
。 ;(2)18;(3)存在唯一正整数
;(2)18;(3)存在唯一正整数 ,使得
,使得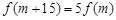 成立。
成立。
 。
。 ;(2)18;(3)存在唯一正整数
;(2)18;(3)存在唯一正整数 ,使得
,使得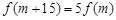 成立。
成立。试题分析:(1)当
 时,
时,  ;
;当
 时,
时,  。
。而
 满足上式。∴
满足上式。∴ 。
。又
 即
即 ,
, 是等差数列。设公差为d。
是等差数列。设公差为d。又
 ,
,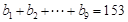
 解得
解得 。
。∴
 6分
6分(2)



 单调递增,
单调递增, 。令
。令 ,得
,得
 。 10分
。 10分(3)
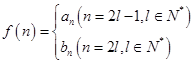
①当
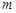 为奇数时,
为奇数时, 为偶数。∴
为偶数。∴ ,
, 。
。②当
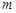 为偶数时,
为偶数时, 为奇数。∴
为奇数。∴ ,
, (舍去)。
(舍去)。综上,存在唯一正整数
 ,使得
,使得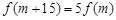 成立。 14分
成立。 14分点评:数列的求和是数列部分的一个重要内容,它往往是数列知识的综合体现,它常用来考查数列的基础知识、基本解题技巧及分析问题、解决问题的能力

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
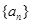 的前n项和为
的前n项和为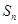 ,令
,令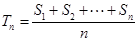 ,称
,称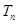 为数列
为数列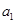 ,
,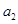 , ,
, ,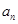 的“理想数”,已知数列
的“理想数”,已知数列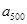 的“理想数”为2004,那么数列12,
的“理想数”为2004,那么数列12, 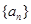 中,
中,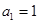 ,
,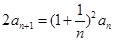 .
.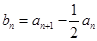 ,求数列
,求数列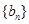 的前
的前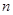 项和
项和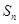 .
. x
x -
- x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
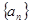 的通项公式为
的通项公式为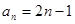 ,数列
,数列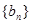 的前n项和为
的前n项和为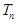 ,且满足
,且满足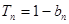
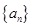 中是否存在使得
中是否存在使得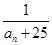 是
是 中,
中, ,若
,若 的取值范围为___________.
的取值范围为___________. ,满足
,满足
 d为常数,我们称
d为常数,我们称 ,则
,则 的个位数( )
的个位数( )  (n∈N*),若前n项的和为
(n∈N*),若前n项的和为 ,则项数为
,则项数为