题目内容
如图,在四棱锥P-ABCD中,底面ABCD是矩形,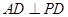 ,BC=1,
,BC=1, ,PD=CD=2.
,PD=CD=2.
(I)求异面直线PA与BC所成角的正切值;
(II)证明平面PDC⊥平面ABCD;
(III)求直线PB与平面ABCD所成角的正弦值。
【考点定位】本小题主要考查异面直线所成的角、平面与平面垂直、直线与平面所成的角等基础知识.,考查空间想象能力、运算求解能力和推理论证能力.
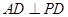 ,BC=1,
,BC=1, ,PD=CD=2.
,PD=CD=2.(I)求异面直线PA与BC所成角的正切值;
(II)证明平面PDC⊥平面ABCD;
(III)求直线PB与平面ABCD所成角的正弦值。

【考点定位】本小题主要考查异面直线所成的角、平面与平面垂直、直线与平面所成的角等基础知识.,考查空间想象能力、运算求解能力和推理论证能力.
(I)2 (2)见解析 (3)

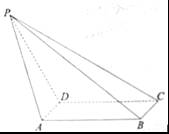
(I)解:如图,在四棱锥P-ABCD中,因为底面ABCD是矩形,所以AD=BC且AD∥BC,又因为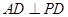 ,故
,故 为异面直线PA与BC所成的角.在
为异面直线PA与BC所成的角.在 中,
中,
所以,异面直线PA与BC所成的角的正切值为2.
(II)证明:由于底面ABCD为矩形,故 ,又由于
,又由于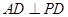 ,
, ,因此
,因此 而
而 .所以
.所以 .
.

(III)解:在平面PDC中,过点P作 交直线CD于点E,连接EB.
交直线CD于点E,连接EB.
由于 ,而直线CD是平面PDC与平面ABCD所成的角.
,而直线CD是平面PDC与平面ABCD所成的角.
在 中,由于PD=CD=2,
中,由于PD=CD=2, ,可得
,可得 .
.
在 中,
中,
由AD∥BC, ,得
,得 ,因此
,因此 .
.
在 中,
中,
在 中,
中,
所以直线PB与平面ABCD所成角的正弦值为
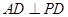 ,故
,故 为异面直线PA与BC所成的角.在
为异面直线PA与BC所成的角.在 中,
中,
所以,异面直线PA与BC所成的角的正切值为2.
(II)证明:由于底面ABCD为矩形,故
 ,又由于
,又由于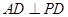 ,
, ,因此
,因此 而
而 .所以
.所以 .
.
(III)解:在平面PDC中,过点P作
 交直线CD于点E,连接EB.
交直线CD于点E,连接EB.由于
 ,而直线CD是平面PDC与平面ABCD所成的角.
,而直线CD是平面PDC与平面ABCD所成的角.在
 中,由于PD=CD=2,
中,由于PD=CD=2, ,可得
,可得 .
.在
 中,
中,
由AD∥BC,
 ,得
,得 ,因此
,因此 .
.在
 中,
中,
在
 中,
中,
所以直线PB与平面ABCD所成角的正弦值为


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
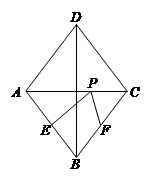





 中,
中, 分别是
分别是 ,
, ,
, 的中心,则
的中心,则 在该正四面体各个面上的射影所有可能的序号是________________.
在该正四面体各个面上的射影所有可能的序号是________________. 

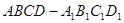 中,
中,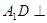 平面
平面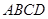 ,底面
,底面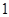 的正方形,侧棱
的正方形,侧棱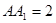 .
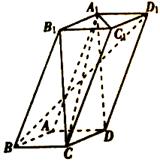
.
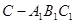 的体积;
的体积;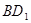 与平面
与平面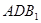 所成角的正弦值;
所成角的正弦值;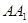 上存在一点
上存在一点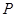 ,使得
,使得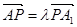 ,当二面角
,当二面角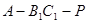 的大小为
的大小为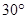 时,求实数
时,求实数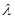 的值.
的值. 表示平面,下面命题中正确的是( )
表示平面,下面命题中正确的是( )
 外一点P,作PO
外一点P,作PO ,垂足为O,连接PA,PB,PC.若PA
,垂足为O,连接PA,PB,PC.若PA PB,PB
PB,PB