题目内容
已知如图几何体,矩形ABCD和矩形ABEF所在平面互相垂直,AF=2AB=2AD,M为AF的中点,BN⊥CE。
(Ⅰ)求证:CF∥平面MBD;
(Ⅱ)求证:CF⊥平面BDN。
(Ⅰ)求证:CF∥平面MBD;
(Ⅱ)求证:CF⊥平面BDN。
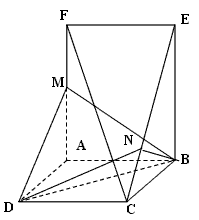
证明:(Ⅰ)连结AC交BD于O,连结OM,
因为M为AF中点,O为AC中点,
所以FC∥MO,
又因为 ,
,
所以FC∥平面MBD;
(Ⅱ)因为正方形ABCD和矩形ABEF所在平面互相垂直,
所以AF⊥平面ABCD,
所以AF⊥BD,
又因为AF 平面ACF,
平面ACF,
所以BD⊥平面ACF,
所以FC⊥BD,
因为正方形ABCD和矩形ABEF,
所以 ,
,
所以AB⊥平面BCE,
所以AB⊥BN,
又因为EF∥AB,
所以EF⊥BN,
又因为EC⊥BN,
所以BN⊥平面CEF,
所以BN⊥FC,
所以CF⊥平面BDN。
因为M为AF中点,O为AC中点,
所以FC∥MO,
又因为
 ,
,所以FC∥平面MBD;
(Ⅱ)因为正方形ABCD和矩形ABEF所在平面互相垂直,
所以AF⊥平面ABCD,
所以AF⊥BD,
又因为AF
 平面ACF,
平面ACF,所以BD⊥平面ACF,
所以FC⊥BD,
因为正方形ABCD和矩形ABEF,
所以
 ,
,所以AB⊥平面BCE,
所以AB⊥BN,
又因为EF∥AB,
所以EF⊥BN,
又因为EC⊥BN,
所以BN⊥平面CEF,
所以BN⊥FC,
所以CF⊥平面BDN。

练习册系列答案
相关题目
 已知如图几何体,矩形ABCD和矩形ABEF所在平面互相垂直,AF=2AB=2AD,M为AF的中点,BN⊥CE.
已知如图几何体,矩形ABCD和矩形ABEF所在平面互相垂直,AF=2AB=2AD,M为AF的中点,BN⊥CE.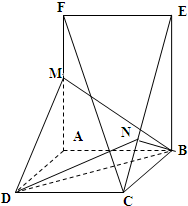 已知如图几何体,矩形ABCD和矩形ABEF所在平面互相垂直,AF=2AB=2AD,M为AF的中点,BN⊥CE.
已知如图几何体,矩形ABCD和矩形ABEF所在平面互相垂直,AF=2AB=2AD,M为AF的中点,BN⊥CE.
