题目内容
设正项等比数列{an}的首项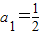 ,前n项和为Sn,且210S30-(210+1)S20+S10=0.
,前n项和为Sn,且210S30-(210+1)S20+S10=0.(Ⅰ)求{an}的通项;
(Ⅱ)求{nSn}的前n项和Tn.
【答案】分析:(Ⅰ)由210S30-(210+1)S20+S10=0得210(S30-S20)=S20-S10,由此可推出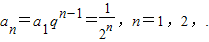
(Ⅱ)由题设知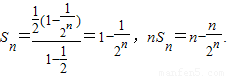 数列{nSn}的前n项和
数列{nSn}的前n项和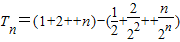 ,
,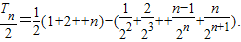 由此可知答案.
由此可知答案.
解答:解:(Ⅰ)由210S30-(210+1)S20+S10=0得210(S30-S20)=S20-S10,
即210(a21+a22+…+a30)=a11+a12+…+a20,
可得210•q10(a11+a12+…+a20)=a11+a12+…+a20.
因为an>0,所以210q10=1,解得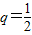 ,因而
,因而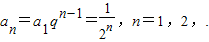
(Ⅱ)由题意知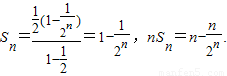
则数列{nSn}的前n项和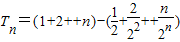 ,
,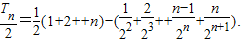
前两式相减,得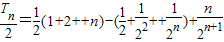 =
=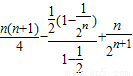 即
即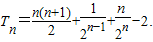
点评:本题考查数列知识的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.
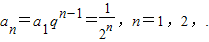
(Ⅱ)由题设知
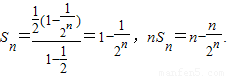 数列{nSn}的前n项和
数列{nSn}的前n项和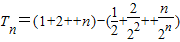 ,
,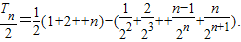 由此可知答案.
由此可知答案.解答:解:(Ⅰ)由210S30-(210+1)S20+S10=0得210(S30-S20)=S20-S10,
即210(a21+a22+…+a30)=a11+a12+…+a20,
可得210•q10(a11+a12+…+a20)=a11+a12+…+a20.
因为an>0,所以210q10=1,解得
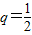 ,因而
,因而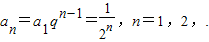
(Ⅱ)由题意知
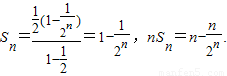
则数列{nSn}的前n项和
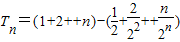 ,
,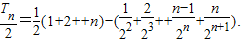
前两式相减,得
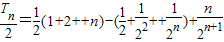 =
=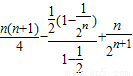 即
即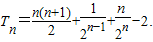
点评:本题考查数列知识的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目