Question

在平面直角坐标系中，已知圆心在第二象限、半径为的圆与直线相切于坐标原点．椭圆与圆的一个交点到椭圆两焦点的距离之和为．

    (1)求圆的方程；

    (2)试探究圆上是否存在异于原点的点，使到椭圆右焦点的距离等于线段的长．若存在，请求出点的坐标；若不存在，请说明理由．

Answer 1

解：（Ⅰ）设圆心坐标为。

则该圆的方程为                  …………………2分

已知该圆与直线相切，那么圆心到该直线的距离等于圆的半径，则

=2，即=4       ①                        …………………5分

又圆与直线切于原点，将点(0，0)代入得m2+n2=8    ②

联立方程①和②组成方程组解得

故圆的方程为(x+2)2+(y-2)2=8                                …………………8分

 （Ⅱ）假设存在点，使得该点到右焦点的距离等于的长。

=5，∴a2=25，则椭圆的方程为                    …………………11分

其焦距c==4，右焦点为(4，0)，那么=4。

即：以右焦点F为顶点，半径为4的圆方程为

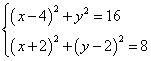   ， 即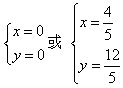：        …………………14分

即存在异于原点的点Q(，)，使得该点到右焦点F的距离等于的长……16分