题目内容
(本小题满分14分)正方体 ,
,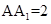 ,E为棱
,E为棱 的中点.
的中点.
(Ⅰ) 求证: ; (Ⅱ) 求证:
; (Ⅱ) 求证: 平面
平面 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
 ,
,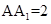 ,E为棱
,E为棱 的中点.
的中点.(Ⅰ) 求证:
 ; (Ⅱ) 求证:
; (Ⅱ) 求证: 平面
平面 ;
;(Ⅲ)求三棱锥
 的体积.
的体积.
(Ⅰ)证明:见解析;(Ⅱ)证明:见解析;
(3) .
.  .
.
(3)
 .
.  .
.本试题主要是考查线线的垂直和线面的平行,以及棱锥的体积的求解综合运用。
(1)结合线面垂直的性质定理和判定定理的综合运用,求证线线垂直。
(2)利用线面平行的判定定理得到证明。
(3)先求解底面的面积,结合锥体的高,得到三棱锥体积。
解: (Ⅰ)证明:连结 ,则
,则 //
// ,
,
∵ 是正方形,∴
是正方形,∴ .∵
.∵ 面
面 ,∴
,∴ .
.
又 ,∴
,∴ 面
面 . ∵
. ∵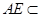 面
面 ,∴
,∴ ,
,
∴ . ………5分
. ………5分
(Ⅱ)证明:作 的中点F,连结
的中点F,连结 .
.
∵ 是
是 的中点,∴
的中点,∴

 ,
,
∴四边形 是平行四边形,∴
是平行四边形,∴ 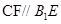 .
.
∵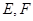 是
是 的中点,∴
的中点,∴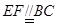 ,
,
又 ,∴
,∴ .
.
∴四边形 是平行四边形,
是平行四边形, //
// ,
,
∵ ,
, ,
,
∴平面 面
面 .
.
又 平面
平面 ,∴
,∴ 面
面 . ………10分
. ………10分
(3) .
.  . ………14分
. ………14分
(1)结合线面垂直的性质定理和判定定理的综合运用,求证线线垂直。
(2)利用线面平行的判定定理得到证明。
(3)先求解底面的面积,结合锥体的高,得到三棱锥体积。
解: (Ⅰ)证明:连结
 ,则
,则 //
// ,
, ∵
 是正方形,∴
是正方形,∴ .∵
.∵ 面
面 ,∴
,∴ .
.又
 ,∴
,∴ 面
面 . ∵
. ∵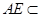 面
面 ,∴
,∴ ,
,∴
 . ………5分
. ………5分(Ⅱ)证明:作
 的中点F,连结
的中点F,连结 .
.∵
 是
是 的中点,∴
的中点,∴

 ,
,∴四边形
 是平行四边形,∴
是平行四边形,∴ 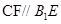 .
.∵
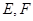 是
是 的中点,∴
的中点,∴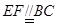 ,
,又
 ,∴
,∴ .
.∴四边形
 是平行四边形,
是平行四边形, //
// ,
,∵
 ,
, ,
,∴平面
 面
面 .
. 又
 平面
平面 ,∴
,∴ 面
面 . ………10分
. ………10分(3)
 .
.  . ………14分
. ………14分
练习册系列答案
相关题目
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 底面
底面 ,
, 是
是 的中点,作
的中点,作 交
交 于点
于点 .
.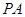 //平面
//平面 ;
; 的大小;
的大小; .
.









 内有一个球与正方体的各个面都相切,经过
内有一个球与正方体的各个面都相切,经过 和
和 作一个截面,正确的截面图是 .
作一个截面,正确的截面图是 .



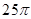
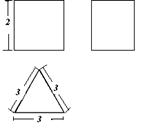
 ,则a=________.
,则a=________.

 ,则该几何体的体积为______________;
,则该几何体的体积为______________;