Question

12．已知过球面上A，B，C的截面到球心O的距离等于球的半径的一半，且AB=BC=CA=3cm，求球的表面积．

Answer 1

分析 设出球的半径，解出△ABC的中心到顶点的距离，然后求出球的半径．然后求出球的表面积．

解答 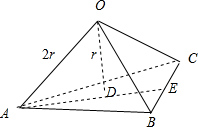解：设球的半径为2r，如图O为球心，E为BC的中点，D是三角形ABC的中心，
那么AO²=OD²+AD²=OD²+$（\frac{2}{3}AE）^{2}$
4r²=r²+（3²-（$\frac{3}{2}$）²）×（$\frac{2}{3}$）²
r=1，
球的半径是：2
所以球的表面积为：4πR²=16π．
故答案为：16π．

点评 本题考查球的半径以及球的体积的求法，考查空间想象能力，是中档题．