题目内容
已知|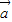 |=3,|
|=3,|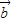 |=2,且3
|=2,且3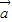 +5
+5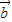 与4
与4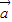 -3
-3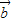 垂直,求
垂直,求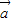 与
与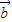 夹角的余弦值.
夹角的余弦值.
【答案】分析:由向量垂直的条件可得(3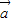 +5
+5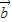 )•(4
)•(4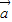 -3
-3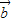 )=0,由此可得
)=0,由此可得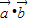 的值,再用向量夹角公式可得答案.
的值,再用向量夹角公式可得答案.
解答:解:∵3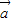 +5
+5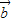 与4
与4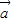 -3
-3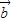 垂直,
垂直,
∴(3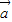 +5
+5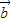 )•(4
)•(4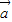 -3
-3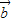 )=0,即12
)=0,即12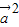 +11
+11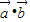 -15
-15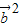 =0,
=0,
又|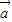 |=3,|
|=3,|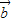 |=2,
|=2,
∴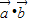 =-
=-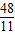 ,
,
则cos<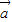 ,
,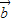 >=
>=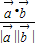 =-
=-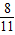 .
.
点评:本题考查向量数量积运算、向量的夹角公式,属基础题.
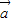 +5
+5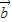 )•(4
)•(4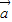 -3
-3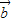 )=0,由此可得
)=0,由此可得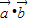 的值,再用向量夹角公式可得答案.
的值,再用向量夹角公式可得答案.解答:解:∵3
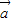 +5
+5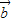 与4
与4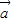 -3
-3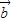 垂直,
垂直,∴(3
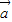 +5
+5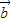 )•(4
)•(4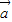 -3
-3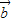 )=0,即12
)=0,即12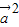 +11
+11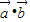 -15
-15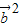 =0,
=0,又|
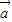 |=3,|
|=3,|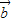 |=2,
|=2,∴
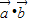 =-
=-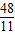 ,
,则cos<
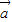 ,
,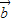 >=
>=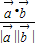 =-
=-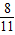 .
.点评:本题考查向量数量积运算、向量的夹角公式,属基础题.

练习册系列答案
相关题目
已知
<α<π,tanα+cotα=-
,则tanα的值为( )
| 3π |
| 4 |
| 10 |
| 3 |
| A、-3 | ||
B、-
| ||
C、-3或-
| ||
D、-
|