题目内容
选修4－1：几何证明选讲
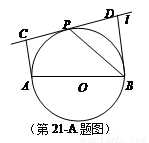
如图，已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连结FB、FC．
（Ⅰ）求证：FB＝FC；
（Ⅱ）求证：FB2＝FA·FD；
（Ⅲ）若AB是△ABC外接圆的直径，∠EAC
＝120°，BC＝6cm，求AD的长．
选修4—1；几何证明选讲
解：（Ⅰ）∵AD平分ÐEAC，∴ÐEAD=ÐDAC．
∵四边形AFBC内接于圆，∴ÐDAC=ÐFBC．
∵ÐEAD=ÐFAB=ÐFCB，∴ÐFBC=ÐFCB，
∴FB=FC．…………………………3分
（Ⅱ）∵ÐFAB=ÐFCB=ÐFBC ，ÐAFB=ÐBFD，
∴ΔFBA∽ΔFDB．∴
，
∴ FB2=FA·FD． ……………………6分
（Ⅲ）∵AB是圆的直径，∴ÐACB=90°．
∵ÐEAC=120°， ∴ÐDAC=
ÐEAC=60°，ÐBAC=60°．∴ÐD=30°．
∵BC= 6， ∴AC=
． ∴AD=2AC=
cm．………………………10分
核心素养学练评系列答案
单元期中期末卷系列答案
（2013•太原一模）选修4一1：几何证明选讲
选修4一1：几何证明选讲
为半圆
的直径，
，
为半圆上一点，过点
，过点
作
于
，交半圆于点
，
．
平分
；
的长．A．选修4－1：几何证明选讲
|
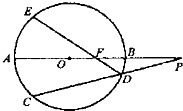
如图，设AB为⊙O的任一条不与直线l垂直的直径，P是⊙O与l的公共点，AC⊥l，BD⊥l，垂足分别为C，D，且PC＝PD．求证：（1）l是⊙O的切线；（2）PB平分∠ABD．
B．选修4－2：矩阵与变换
（本小题满分10分）
已知点A在变换：T：→＝作用后，再绕原点逆时针旋转90°，得到点B．若点B坐标为(－3，4)，求点A的坐标．
C．选修4－4：坐标系与参数方程
（本小题满分10分）
求曲线C1：被直线l：y＝x－所截得的线段长．
D．选修4－5：不等式选讲
（本小题满分10分）
已知a、b、c是正实数，求证：≥．
ABC中的两条角平分线
和
相交于
，
B=60
，
在
上，且
。 
四点共圆；