题目内容
数 的单调递增区间为( )
的单调递增区间为( )
| A.(-∞,1) | B.(2,+∞) | C.(-∞, ) ) | D.( ,+∞) ,+∞) |
A
解析试题分析:由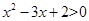 得:
得: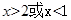 ,
,
令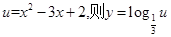 ,因为
,因为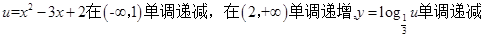 ,所以
,所以 的单调递增区间为(-∞,1)。
的单调递增区间为(-∞,1)。
考点:复合函数的单调性。
点评:判断复合函数的单调性,只需要满足四个字:同增异减,但一定要注意先求函数的定义域。本题易错的地方是:忘记求定义域而导致选错误答案C。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
一次函数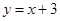 与
与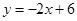 的图象的交点组成的集合是( )
的图象的交点组成的集合是( )
A. | B. | C. | D. |
若函数 在
在 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
下列说法中:
① 若 (其中
(其中 )是偶函数,则实数
)是偶函数,则实数 ;
;
②  既是奇函数又是偶函数;
既是奇函数又是偶函数;
③ 函数 的减区间是
的减区间是 ;
;
④ 已知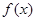 是定义在
是定义在 上的不恒为零的函数,且对任意的
上的不恒为零的函数,且对任意的 都满足
都满足 ,则
,则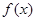 是奇函数。
是奇函数。
其中正确说法的序号是( )
| A.①②④ | B.①③④ |
| C.②③④ | D.①②③ |
函数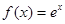 (
(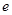 为自然对数的底数)对任意实数
为自然对数的底数)对任意实数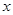 、
、 ,都有( )
,都有( )
A.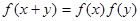 | B.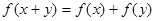 |
C.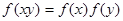 | D.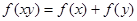 |
已知函数 ,且
,且 ,则实数
,则实数 的值为( )
的值为( )
A. | B. | C. 或 或 | D. 或 或 或 或 |
已知函数 满足:x≥4,则
满足:x≥4,则 =
=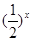 ;当x<4时
;当x<4时 =
=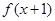 ,则
,则 =
=
A.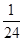 | B.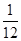 | C.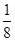 | D.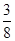 |
已知定义在 上的函数
上的函数 满足
满足 ,且
,且 ,
,  ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则
,则 等于( )
等于( )
| A.4 | B.5 | C.6 | D.7 |
若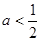 ,则化简
,则化简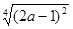 的结果是( )
的结果是( )
A.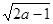 | B.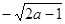 | C.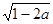 | D.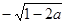 |