题目内容
根据函数单调性定义，证明函数f（x）=-
+1在（-∞，0）上是增函数．
| 2 |
| x |
设x1＜x2＜0，
则f（x1）-f（x2）=-
+1-（-
+1）=
，
∵x1＜x2＜0，∴x1-x2＜0，x1x2＞0，
∴f（x1）-f（x2）＜0，即f（x1）＜f（x2），
∴函数f（x）=-
+1在（-∞，0）上是增函数．
则f（x1）-f（x2）=-
| 2 |
| x1 |
| 2 |
| x2 |
| 2(x1-x2) |
| x1x2 |
∵x1＜x2＜0，∴x1-x2＜0，x1x2＞0，
∴f（x1）-f（x2）＜0，即f（x1）＜f（x2），
∴函数f（x）=-
| 2 |
| x |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
)上是减函数，在[
在区间(－1，1)上是增函数．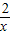
+1在（-∞，0）上是增函数．