题目内容
如图△ABC是等腰直角三角形，∠B=90°，D是BC边上的中点，BE⊥AD，延长BE交AC于F，连接DF，求证：∠ADB=∠FDC．分析：根据等角的余角相等，得到∠ABF=∠ADB，根据两个角对应相等，得到两个三角形相似，相似三角形的对应角相等，得到∠ABF=∠ADB，通过等量代换得到要证的结果．
解答：
证明：∵BE⊥AD，∠B=90°，
∴∠ABF=∠ADB
∵∠BAC=∠C
∠AFB=∠CFD，
∴△ABF∽△CDF，
∴∠ABF=∠CDF，
∵∠ABF=∠ADB，
∴∠ADB=∠FDC
证明：∵BE⊥AD，∠B=90°，∴∠ABF=∠ADB
∵∠BAC=∠C
∠AFB=∠CFD，
∴△ABF∽△CDF，
∴∠ABF=∠CDF，
∵∠ABF=∠ADB，
∴∠ADB=∠FDC
点评：本题是一个通过三角形相似来证明对应角相等的题目，这种题目在解题时注意应用角间的等量关系和等量代换，本题是一个基础题．
练习册系列答案
名校课堂系列答案
相关题目
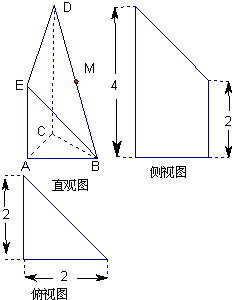如图，是某直三棱柱（侧棱与底面垂直）被削 去上底后的直观图与三视图的侧视图、俯视图．在直观图中，M是BD的中点．侧视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示．
