题目内容
已知复数z=sinθ+2i(0≤θ≤
),且z-(
+i)=
+2i,求倾斜角为θ并经过点(-6,0)的直线l与曲线y=x2所围成的图形的面积.
| π |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
. |
| z |
分析:本题首先根据已知复数z=sinθ+2i(0≤θ≤
),且z-(
+i)=
+2i,求出角θ;然后写出直线l的方程,再利用定积分即可求出面积.
| π |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
. |
| z |
解答:解:∵z=sinθ+2i,∴
=sini-2i,
有∵z-(
+i)=
+2i,
∴sinθ+2i-(
+i)=
(sinθ-2i)+2i,∴sinθ-
+i=
sinθ+i,
∴sinθ=
,
∵0≤θ≤
,∴θ=
,
∴直线l的斜率k=tan
=1,
又∵直线l过点(-6,0),∴直线l的方程为y=x+6.
联立
,解之得x=-2,或x=3.
所要求的面积S=
(x+6-x2)dx=((
x2+6x-
x3)
=
.
. |
| z |
有∵z-(
| ||
| 4 |
| 1 |
| 2 |
. |
| z |
∴sinθ+2i-(
| ||
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
∴sinθ=
| ||
| 2 |
∵0≤θ≤
| π |
| 2 |
| π |
| 4 |
∴直线l的斜率k=tan
| π |
| 4 |
又∵直线l过点(-6,0),∴直线l的方程为y=x+6.
联立
|
所要求的面积S=
| ∫ | 3 -2 |
| 1 |
| 2 |
| 1 |
| 3 |
| | | 3 -2 |
| 125 |
| 6 |
点评:本题综合考查了复数、直线的方程及利用定积分求面积,熟练利用以上有关知识及方法进行计算是解决问题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
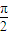 <θ<π),求z的共轭复数
<θ<π),求z的共轭复数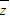 的辐角主值.
的辐角主值.