题目内容
已知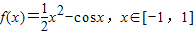
，则导函数f′（x）是（ ）A．仅有最小值的奇函数
B．既有最大值，又有最小值的偶函数
C．仅有最大值的偶函数
D．既有最大值，又有最小值的奇函数
【答案】分析：求出f′（x），利用导数可判断其单调性，通过单调性即可求出其最大最小值；再用定义可判断其奇偶性，从而得出答案．
解答：解：f′（x）=x+sinx，令g（x）=x+sinx，则g′（x）=1+cosx．
当x∈[-1，1]时，g′（x）＞0，所以f′（x）=g（x）在[-1，1]上单调递增，
所以f′（-1）≤f′（x）≤f′（1），即-1-sin1≤f′（x）≤1+sin1．
又f′（-x）=-x+sin（-x）=-x-sinx=-（x+sinx）=-f′（x），所以f′（x）是奇函数．
故选D．
点评：本题考查了应用导数求函数最值问题，奇偶性的判断，难度不大．掌握相关基础知识是解决该题的关键．
解答：解：f′（x）=x+sinx，令g（x）=x+sinx，则g′（x）=1+cosx．
当x∈[-1，1]时，g′（x）＞0，所以f′（x）=g（x）在[-1，1]上单调递增，
所以f′（-1）≤f′（x）≤f′（1），即-1-sin1≤f′（x）≤1+sin1．
又f′（-x）=-x+sin（-x）=-x-sinx=-（x+sinx）=-f′（x），所以f′（x）是奇函数．
故选D．
点评：本题考查了应用导数求函数最值问题，奇偶性的判断，难度不大．掌握相关基础知识是解决该题的关键．
练习册系列答案
相关题目
已知f（x）=
x2-cosx，x∈[-1，1]，则导函数f′（x）是（ ）
| 1 |
| 2 |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数也不是偶函数 |
，则导函数f′（x）是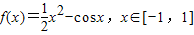
，则导函数f′（x）是（ ）
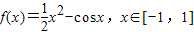，则导函数f′（x）是（ ）