题目内容
已知三个不等式:(1)ab<0;(2)-
<-
;(3)bc>ad,以其中两个作为条件,余下的作为结论,则可以组成
| c |
| a |
| d |
| b |
0个
0个
正确命题.分析:根据不等式的性质来进行证明即可,不等式两边同乘(或除)一个正数不等号的方向不改变,同乘(或除)一个负数,不等号的方向改变,利用此关系对三式的三同组合进行验证来确定即可得到结论.
解答:解:研究(1)(2)⇒(3),由于ab<0,将 -
<-
两边同乘以-ab得bc<ad,故(1)(2)⇒(3)不成立;
研究(1)(3)⇒(2),由于ab<0,故bc>ad两边同除以-ab得-
>-
,故(1)(3)⇒(2)不成立;
研究(2)(3)⇒(1),由于 -
<-
两边同乘以-ab得bc>ad,由不等式的性质知必有-ab<0即ab>0,故(2)(3)⇒(1)不成立.
由上证知,以其中两个作为条件,余下一个作为结论组成命题,可以组成0个正确命题,
故答案为:0个.
| c |
| a |
| d |
| b |
研究(1)(3)⇒(2),由于ab<0,故bc>ad两边同除以-ab得-
| c |
| a |
| d |
| b |
研究(2)(3)⇒(1),由于 -
| c |
| a |
| d |
| b |
由上证知,以其中两个作为条件,余下一个作为结论组成命题,可以组成0个正确命题,
故答案为:0个.
点评:本题主要考查了不等式的基本性质,以及命题真假的判定,不等式的性质有①若a<b,b<c,则a<c,②如果a>b,那么a+c>b+c,a-c>b-c,③如果a>b,且c>0,那么ac>bc,
>
,如果a>b,且c<0,那么ac<bc,
<
,属于基础题.
| a |
| c |
| b |
| c |
| a |
| c |
| b |
| c |

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
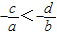 ;(3)bc>ad,以其中两个作为条件,余下的作为结论,则可以组成 正确命题.
;(3)bc>ad,以其中两个作为条件,余下的作为结论,则可以组成 正确命题.