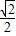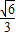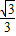题目内容
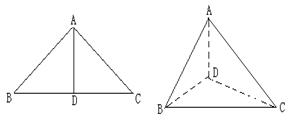
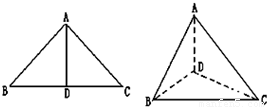
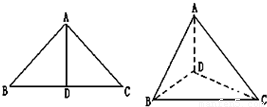
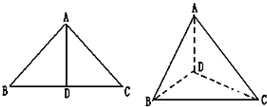 如图,以等腰三角形ABC的斜边BC上的高AD位折痕,将△ABD和△ACD折起,使折起后的△ABC成等边三角形,则二面角C-AB-D的余弦值等于( )
如图,以等腰三角形ABC的斜边BC上的高AD位折痕,将△ABD和△ACD折起,使折起后的△ABC成等边三角形,则二面角C-AB-D的余弦值等于( )分析:设AB中点为E,AD=a,连接CE,DE,则∠CED为所求二面角,证明CD⊥DE,即可求得二面角C-AB-D的余弦值.
解答: 解:设AB中点为E,AD=a,连接CE,DE,
解:设AB中点为E,AD=a,连接CE,DE,
∵AD=DB,CA=CB
∴AB⊥DE,AB⊥CE
∴∠CED为所求二面角,
∵AD=a,∴DE=
a,CE=
AB=
a,CD=a,
∴CE2=CD2+DE2
∴CD⊥DE
∴cos∠CED=
=
=
故选D.
 解:设AB中点为E,AD=a,连接CE,DE,
解:设AB中点为E,AD=a,连接CE,DE,∵AD=DB,CA=CB
∴AB⊥DE,AB⊥CE
∴∠CED为所求二面角,
∵AD=a,∴DE=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴CE2=CD2+DE2
∴CD⊥DE
∴cos∠CED=
| DE |
| CE |
| ||||
|
| ||
| 3 |
故选D.
点评:本题考查面面角,考查学生的计算能力,正确作出面面角是关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论: ①
①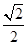 B.
B. C.
C.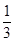 D.
D.