题目内容
(本小题满分12分)
已知点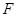 是椭圆
是椭圆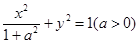 的右焦点,点
的右焦点,点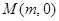 、
、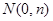 分别是
分别是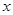 轴、
轴、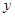 轴上的动点,且满足
轴上的动点,且满足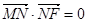 .若点
.若点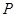 满足
满足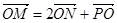 .
.
(1)求点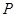 的轨迹
的轨迹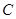 的方程;
的方程;
(2)设过点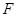 任作一直线与点
任作一直线与点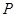 的轨迹交于
的轨迹交于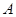 、
、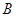 两点,直线
两点,直线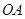 、
、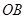 与直线
与直线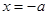 分别交于点
分别交于点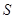 、
、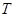 (
(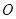 为坐标原点),试判断
为坐标原点),试判断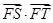 是否为定值?若是,求出这个定值;若不是,请说明理由.
是否为定值?若是,求出这个定值;若不是,请说明理由.
【答案】
(1)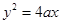 ;(2)
;(2) 的值是定值,且定值为
的值是定值,且定值为 .
.
【解析】第一问中利用向量的数量积为0,也就是向量的垂直关系式得到由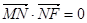 ,得
,得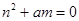 ,然后设所求点的坐标
,然后设所求点的坐标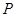 的坐标为
的坐标为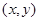 ,由
,由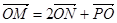 ,有
,有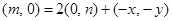
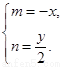 代入
代入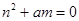 ,得
,得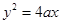 ,采用了消元的思想得到轨迹方程。
,采用了消元的思想得到轨迹方程。
第二问中,设出直线方程,利用直线与抛物线联立方程组得到 为定值。
为定值。
解:(1)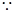 椭圆
椭圆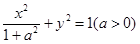 右焦点
右焦点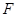 的坐标为
的坐标为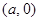 ,………………1分
,………………1分
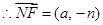 .
.
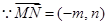 ,
,
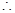 由
由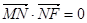 ,得
,得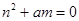 .
…………………………2分
.
…………………………2分
设点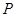 的坐标为
的坐标为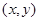 ,由
,由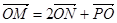 ,有
,有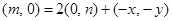 ,
,
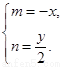 代入
代入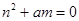 ,得
,得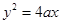 . …………………………4分
. …………………………4分
(2)(法一)设直线 的方程为
的方程为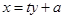 ,
, .
.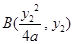 ,
,
则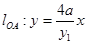 ,
, .
………………………………5分
.
………………………………5分
由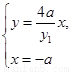 ,得
,得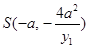 ,
同理得
,
同理得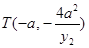 .…………………………7分
.…………………………7分
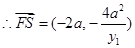 ,
,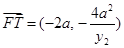 ,则
,则 . ………8分
. ………8分
由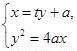 ,得
,得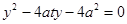 ,
,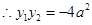 . ……………………9分
. ……………………9分
则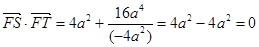 .
…………………………11分
.
…………………………11分
因此, 的值是定值,且定值为
的值是定值,且定值为 . ………………………12分
. ………………………12分
(法二)①当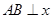 时,
时,
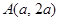 .
.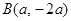 ,则
,则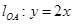 ,
,  .
.
由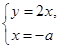 得点
得点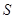 的坐标为
的坐标为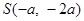 ,则
,则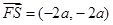 .
.
由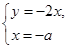 得点
得点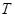 的坐标为
的坐标为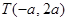 ,则
,则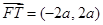 .
.

 .
………………………………………6分
.
………………………………………6分
②当 不垂直
不垂直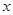 轴时,设直线
轴时,设直线 的方程为
的方程为 ,
,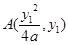 .
.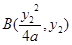 ,同解法一,得
,同解法一,得 . ……………8分
. ……………8分
由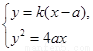 ,得
,得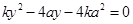 ,
,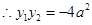 .……………………10分
.……………………10分
则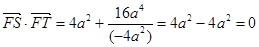 .
…………………………11分
.
…………………………11分
因此, 的值是定值,且定值为
的值是定值,且定值为 . …………………………12分
. …………………………12分

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目