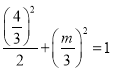题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 在直线
在直线![]() 上.数列
上.数列![]() 满足
满足![]() 且
且![]() ,前9项和为153.
,前9项和为153.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() 及使不等式
及使不等式![]() 对一切
对一切![]() 都成立的最小正整数
都成立的最小正整数![]() 的值;
的值;
(3)设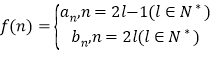 ,问是否存在
,问是否存在![]() ,使得
,使得![]() 成立?若不存在,请说明理由.
成立?若不存在,请说明理由.
【答案】(1) ![]() .
.
(2)1009.
(3)m=11.
【解析】分析:(1)运用数列的通项公式和前n项和的关系,即可得到数列![]() 的通项公式;运用等差数列的通项和求和公式,求出公差,即可得到数列
的通项公式;运用等差数列的通项和求和公式,求出公差,即可得到数列![]() 的通项公式;
的通项公式;
(2)化简![]() ,运用裂项相消法求和,求出数列
,运用裂项相消法求和,求出数列![]() 的前n项和为
的前n项和为![]() ,再由数列的单调性,即可得出k的最小值;
,再由数列的单调性,即可得出k的最小值;
(3)分m为奇数和m为偶数,分别利用条件![]() ,求出m的值,可得结论.
,求出m的值,可得结论.
详解:(1)![]()
(2)![]()
![]()
![]()
![]()
(3)当![]() 为奇数时,
为奇数时,![]()
当![]() 为偶数时,
为偶数时,![]()
![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目