题目内容
过点M(4,2)作x轴的平行线被抛物线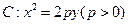 截得的弦长为
截得的弦长为 。
。
(I)求p的值;
(II)过抛物线C上两点A,B分别作抛物线C的切线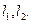
(i)若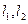 交于点M,求直线AB的方程;
交于点M,求直线AB的方程;
(ii)若直线AB经过点M,记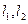 的交点为N,当
的交点为N,当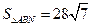 时,求点N的坐标
时,求点N的坐标
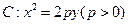 截得的弦长为
截得的弦长为 。
。(I)求p的值;
(II)过抛物线C上两点A,B分别作抛物线C的切线
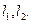
(i)若
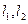 交于点M,求直线AB的方程;
交于点M,求直线AB的方程;(ii)若直线AB经过点M,记
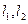 的交点为N,当
的交点为N,当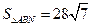 时,求点N的坐标
时,求点N的坐标(I)2
(II)
(i)2x-y=0
(ii)点N的坐标为(—2,—6)或(10,18)
解:(I)由已知得点 在抛物线
在抛物线 上,…………2分
上,…………2分
代入得8=4p,故p="2." …………4分
(II)设 直线AB方程为
直线AB方程为

则 …………6分
…………6分

故抛物线在A,B两点处的切线斜率分别为
故在A,B点处的切线方程分别为
于是 …………8分
…………8分
(i)由题意得M(4,2)是 的交点,
的交点,
故 …………9分
…………9分
(ii)由题意得 ,
,

故 …………11分
…………11分

 …………13分
…………13分
故
即 , …………14分
, …………14分
故点N的坐标为(—2,—6)或(10,18). …………15分
 在抛物线
在抛物线 上,…………2分
上,…………2分代入得8=4p,故p="2." …………4分
(II)设
 直线AB方程为
直线AB方程为

则
 …………6分
…………6分
故抛物线在A,B两点处的切线斜率分别为

故在A,B点处的切线方程分别为

于是
 …………8分
…………8分(i)由题意得M(4,2)是
 的交点,
的交点,故
 …………9分
…………9分(ii)由题意得
 ,
,
故
 …………11分
…………11分
 …………13分
…………13分故

即
 , …………14分
, …………14分故点N的坐标为(—2,—6)或(10,18). …………15分

练习册系列答案
相关题目
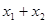 =6,那么
=6,那么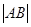 = ( *** )
= ( *** ) 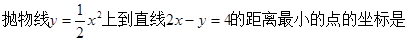 ( )
( )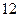 分)已知抛物线的顶点在坐标原点,焦点在
分)已知抛物线的顶点在坐标原点,焦点在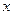 轴正半轴,抛物线上一点
轴正半轴,抛物线上一点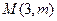 到焦点的距离为
到焦点的距离为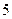 ,求
,求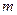 的值及抛物线方程.
的值及抛物线方程. 的焦点坐标为( )
的焦点坐标为( ) ,0)
,0) )
)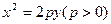 的焦点与椭圆
的焦点与椭圆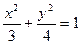 的上焦点重合,
的上焦点重合,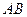 是过抛物线焦点的动弦,直线
是过抛物线焦点的动弦,直线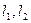 是抛物线两条分别切于
是抛物线两条分别切于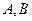 的切线,求
的切线,求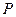 到点
到点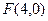 的距离比它到直线
的距离比它到直线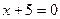 的距离少1,则动点
的距离少1,则动点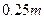 ,靠近中轴线的车道为快车道,两侧的车道为慢车道,则车辆通过隧道时,慢车道的限制高度为 .(精确到
,靠近中轴线的车道为快车道,两侧的车道为慢车道,则车辆通过隧道时,慢车道的限制高度为 .(精确到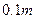 )
)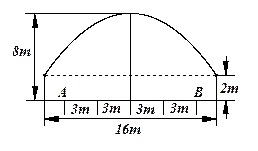
 的顶点,过点D(0,4)的直线
的顶点,过点D(0,4)的直线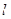 交抛物线
交抛物线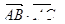 等于( )
等于( )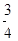 B.0 C.-3 D.
B.0 C.-3 D.