题目内容
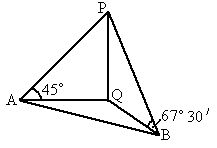
空中有一气球,在它的正西方A点测得它的仰角为45°,同时在它南偏东60°的B点,测得它的仰角为30°,若A、B两点间的距离为266米,这两个观测点均离地1米,那么测量时气球到地面的距离是
(
+1)米
| 266 | ||
|
(
+1)米
.| 266 | ||
|
分析:设气球Q的正下方理底面1米的地方为点O,则由题意可得∠AOB=150°,AB=266米,∠PAO=45°,∠PBO=30°.设PO=x,则由直角三角形中的边角关系可得OA和OB的值.△AOB中,由余弦定理可得 x的值,则x+1为所求.
解答:解:设气球Q的正下方理底面1米的地方为点O,则由题意可得∠AOB=90°+60°=150°,AB=266米,
∠PAO=45°,∠PBO=30°.
设PO=x,则由直角三角形中的边角关系可得OA=x,OB=
=
x.
△AOB中,由余弦定理可得 AB2=2662=AO2+BO2-2AO•BO•cos∠AOB=x2+3x2-2
x2 cos150°,
解得 x=
米,故气球到地面的距离是 (
+1)米,
故答案为(
+1 )米.
∠PAO=45°,∠PBO=30°.
设PO=x,则由直角三角形中的边角关系可得OA=x,OB=
| x |
| tan30° |
| 3 |
△AOB中,由余弦定理可得 AB2=2662=AO2+BO2-2AO•BO•cos∠AOB=x2+3x2-2
| 3 |
解得 x=
| 266 | ||
|
| 266 | ||
|
故答案为(
| 266 | ||
|
点评:本题主要考查解三角形的实际应用,直角三角形中的边角关系,要注意气球到地面的距离是OQ+1,属于
中档题.
中档题.

练习册系列答案
相关题目
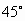 ,同时在它的正南偏东的B点,测得它的仰角为
,同时在它的正南偏东的B点,测得它的仰角为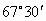 ,A,B两点的距离为266m,这两测点均离地1m,问当测量时这气球离地面多远?
,A,B两点的距离为266m,这两测点均离地1m,问当测量时这气球离地面多远?
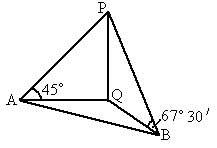
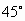 ,同时在它的正南偏东的B点,测得它的仰角为
,同时在它的正南偏东的B点,测得它的仰角为 ,A,B两点的距离为266m,这两测点均离地1m,问当测量时这气球离地面多远?
,A,B两点的距离为266m,这两测点均离地1m,问当测量时这气球离地面多远?