题目内容
已知集合A={x||x-2|＞a（a＞0）}，B={x|x2-5x-6＜0}；若A∩B=∅，求实数a的取值范围．
解：由|x-2|＞a 得 x-2＞a，或 x-2＜-a，即x＞a+2，或x＜2-a．-------
由x2-5x-6＜0 得-1＜x＜6．-------
由于 A∩B=∅，∴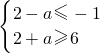
，-------
解得 a≥4．----
分析：解绝对值不等式求得A，解一元二次不等式求得B，再根据A∩B=∅，求实数a的取值范围．
点评：本题主要考查绝对值不等式、一元二次不等式的解法，两个集合的交集的定义，属于基础题．
由x2-5x-6＜0 得-1＜x＜6．-------
由于 A∩B=∅，∴
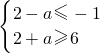，-------解得 a≥4．----
分析：解绝对值不等式求得A，解一元二次不等式求得B，再根据A∩B=∅，求实数a的取值范围．
点评：本题主要考查绝对值不等式、一元二次不等式的解法，两个集合的交集的定义，属于基础题．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目