题目内容
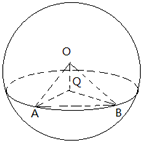 如图,点A、B都在半径为2的球上,圆Q是过A、B两点的截面,若A、B的球面距离为π,OQ=1,则三棱锥Q-ABO的体积等于
如图,点A、B都在半径为2的球上,圆Q是过A、B两点的截面,若A、B的球面距离为π,OQ=1,则三棱锥Q-ABO的体积等于
- A.

- B.

- C.

- D.3
C
分析:先根据A、B两点的球面距离为π,推出∠AOB= ,从而在直角三角形ABO中求出斜边AB的长,结合棱AQ,BQ的长,推出三棱锥的底面面积,然后求三棱锥Q-ABO的体积.
,从而在直角三角形ABO中求出斜边AB的长,结合棱AQ,BQ的长,推出三棱锥的底面面积,然后求三棱锥Q-ABO的体积.
解答:由题意,A、B两点的球面距离为π.所以∠AOB= ,
,
在直角三角形ABO中,OA=OB=2,所以AB=2 ,
,
在直角三角形AQO和三角形BQO中,OA=OB=2,OQ=1,所以AQ=BQ= ,
,
在等腰三角形ABO中,底AB边长的高为1,
所以三棱锥Q-ABO的体积体积:V= ×
× AB×1×OQ=
AB×1×OQ= ,
,
故选C
点评:本题考查球内接多面体、棱锥的体积,考查学生分析问题解决问题的能力,是基础题.
分析:先根据A、B两点的球面距离为π,推出∠AOB=
 ,从而在直角三角形ABO中求出斜边AB的长,结合棱AQ,BQ的长,推出三棱锥的底面面积,然后求三棱锥Q-ABO的体积.
,从而在直角三角形ABO中求出斜边AB的长,结合棱AQ,BQ的长,推出三棱锥的底面面积,然后求三棱锥Q-ABO的体积.解答:由题意,A、B两点的球面距离为π.所以∠AOB=
 ,
,在直角三角形ABO中,OA=OB=2,所以AB=2
 ,
,在直角三角形AQO和三角形BQO中,OA=OB=2,OQ=1,所以AQ=BQ=
 ,
,在等腰三角形ABO中,底AB边长的高为1,
所以三棱锥Q-ABO的体积体积:V=
 ×
× AB×1×OQ=
AB×1×OQ= ,
,故选C
点评:本题考查球内接多面体、棱锥的体积,考查学生分析问题解决问题的能力,是基础题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
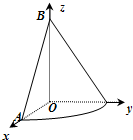 如图,直角三角形OAB的直角顶点O是空间坐标系O-xyz的原点,点A在Ox轴正半轴上,|OA|=1;点B在Oz轴正半轴上,|OB|=2.我们称△OAB绕Oz轴逆时针旋转
如图,直角三角形OAB的直角顶点O是空间坐标系O-xyz的原点,点A在Ox轴正半轴上,|OA|=1;点B在Oz轴正半轴上,|OB|=2.我们称△OAB绕Oz轴逆时针旋转| π |
| 2 |
| A、该四分之一圆锥体主视图和左视图的图形是全等的直角三角形 | ||
B、该四分之一圆锥体俯视图的图形是一个圆心角为
| ||
| C、该四分之一圆锥体主视图、左视图和俯视图的图形都是扇形 | ||
| D、该四分之一圆锥体主视图的图形面积大于俯视图的图形面积 |
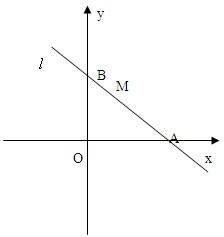 已知直线l过点M(1,2),且直线l与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线l与坐标轴的交点都在正半轴上)
已知直线l过点M(1,2),且直线l与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线l与坐标轴的交点都在正半轴上)
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.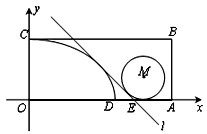 在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上(如图),且OC=1,OA=a+1(a>1),点D在边OA上,满足OD=a.分别以OD、OC为长、短半轴的椭圆在矩形及其内部的部分为椭圆弧CD.直线l:y=-x+b与椭圆弧相切,与OA交于点E.
在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上(如图),且OC=1,OA=a+1(a>1),点D在边OA上,满足OD=a.分别以OD、OC为长、短半轴的椭圆在矩形及其内部的部分为椭圆弧CD.直线l:y=-x+b与椭圆弧相切,与OA交于点E.