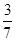题目内容
在一个盒子中有大小一样的7个球,球上分别标有数字1,1,2,2,2,3,3.现从盒子中同时摸出3个球,设随机变量X为摸出的3个球上的数字和.(1)求概率P(X≥7);
(2)求X的概率分布列,并求其数学期望E(X).
【答案】分析:(1)X≥7表示取到2个2号球和1个3号球,或取到1个2号球和2个3号球,或取到1个1号球2个3号球,由此能求出P(X≥7).
(2)由题设知X的可能取值分别为4,5,6,7,8,分别求出P(X=4),P(X=5),P(X=6),P(X=7),P(X=8).由此能求出X的分布列和EX.
解答:解:(1)X≥7表示取到2个2号球和1个3号球,或取到1个2号球和2个3号球,或取到1个1号球2个3号球,
∴P(X≥7)=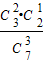 +
+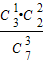 +
+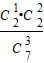 =
=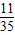 .
.
(2)由题设知X的可能取值分别为4,5,6,7,8,
P(X=4)=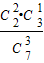 =
=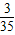 ,
,
P(X=5)=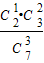 +
+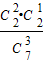 =
=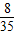 ,
,
P(X=6)=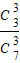 +
+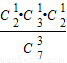 =
=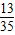 ,
,
P(X=7)=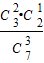 +
+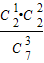 =
=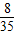 ,
,
P(X=8)=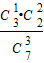 =
=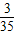 .
.
∴X的分布列为:
∴EX=4×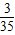 +5×
+5×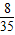 +6×
+6×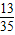 +7×
+7×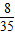 +8×
+8×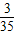 =6.
=6.
点评:本题考查离散型随机变量的分布列和数学期望,是中档题.在历年高考中都是必考题型.解题时要认真审题,仔细解答,注意概率知识的灵活运用.
(2)由题设知X的可能取值分别为4,5,6,7,8,分别求出P(X=4),P(X=5),P(X=6),P(X=7),P(X=8).由此能求出X的分布列和EX.
解答:解:(1)X≥7表示取到2个2号球和1个3号球,或取到1个2号球和2个3号球,或取到1个1号球2个3号球,
∴P(X≥7)=
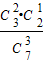 +
+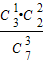 +
+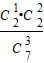 =
=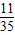 .
.(2)由题设知X的可能取值分别为4,5,6,7,8,
P(X=4)=
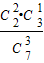 =
=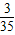 ,
,P(X=5)=
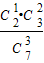 +
+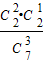 =
=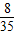 ,
,P(X=6)=
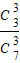 +
+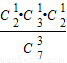 =
=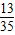 ,
,P(X=7)=
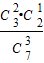 +
+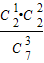 =
=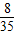 ,
,P(X=8)=
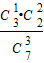 =
=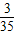 .
.∴X的分布列为:
| X | 4 | 5 | 6 | 7 | 8 |
| P | 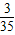 | 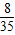 | 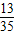 | 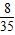 | 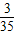 |
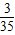 +5×
+5×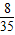 +6×
+6×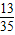 +7×
+7×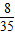 +8×
+8×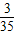 =6.
=6.点评:本题考查离散型随机变量的分布列和数学期望,是中档题.在历年高考中都是必考题型.解题时要认真审题,仔细解答,注意概率知识的灵活运用.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
. =5的概率;
=5的概率; 个球,其中
个球,其中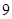 个红球,
个红球,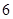 个白球,甲、乙两人各摸一球,不放回,则在甲摸出红球的条件下,乙摸出白球的概率为( )
个白球,甲、乙两人各摸一球,不放回,则在甲摸出红球的条件下,乙摸出白球的概率为( )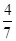 B.
B.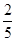 C.
C.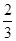 D.
D.