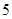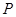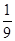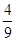题目内容
在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中有放回地先后摸出两球,所得分数分别记为 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
.
(1)求随机变量 =5的概率;
=5的概率;
(2)求随机变量 的分布列和数学期望.
的分布列和数学期望.
【答案】
(1)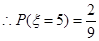
(2)随机变量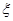 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
因此,数学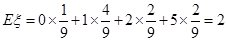
【解析】
试题分析:解(Ⅰ) 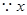 、
、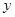 可能的取值为
可能的取值为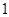 、
、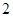 、
、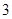 ,
,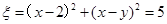 ,
,
且当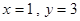 或
或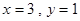 时,
时,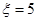 ,又有放回摸两球的所有情况有
,又有放回摸两球的所有情况有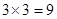 种,
种,
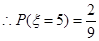 .
6分
.
6分
(Ⅱ) 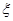 的所有取值为
的所有取值为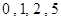 .
.
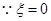 时,只有
时,只有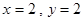 这一种情况.
这一种情况.
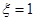 时,有
时,有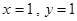 或
或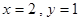 或
或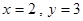 或
或 四种情况,
四种情况,
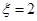 时,有
时,有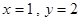 或
或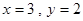 两种情况.
两种情况.
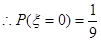 ,
,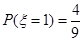 ,
,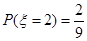 , 8分
, 8分
则随机变量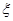 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
因此,数学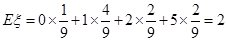 .
12分
.
12分
考点:古典概型
点评:主要四考查了古典概型概率的运用,以及分布列的求解属于中档题。

练习册系列答案
相关题目