题目内容
若m,n∈{-2,-1,0,1,2,4},则
+
=1表示焦点在x轴上的圆锥曲线的概率为
.
| x2 |
| m |
| y2 |
| n |
| 1 |
| 4 |
| 1 |
| 4 |
分析:m和n的所有的可能取值共有6×6=36个,从中数出能使方程是焦点在x轴上的双曲线的选法,即m和n都为正的且m>n选法数,或m是正,n为负的选法数,最后由古典概型的概率计算公式即可得其概率.
解答:解:设(m,n)表示m,n的取值组合,则表示焦点在x轴上的圆锥曲线的取值的所有情况有-6×6=36个,
其中能使方程是焦点在x轴上的双曲线的必须满足m和n都为正的且m>n选法数,或m是正,n为负的选法数,
有
+3×2共9个
∴此方程是焦点在x轴上的双曲线方程的概率为
=
.
故答案为:
.
其中能使方程是焦点在x轴上的双曲线的必须满足m和n都为正的且m>n选法数,或m是正,n为负的选法数,
有
| C | 2 3 |
∴此方程是焦点在x轴上的双曲线方程的概率为
| 9 |
| 36 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查了古典概型概率的求法,椭圆、双曲线、抛物线的标准方程,列举法计数的技巧,准确计数是解决本题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
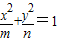 表示焦点在x轴上的圆锥曲线的概率为 .
表示焦点在x轴上的圆锥曲线的概率为 .