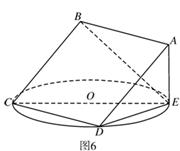
题目内容
如图6,正方形![]() 所在平面与圆
所在平面与圆![]() 所在平面相交于
所在平面相交于![]() ,线段
,线段![]() 为圆
为圆![]() 的弦,
的弦,![]() 垂直于圆
垂直于圆![]() 所在平面,垂足
所在平面,垂足![]() 是圆
是圆![]() 上异于
上异于![]() 、
、![]() 的点,
的点,![]() ,圆
,圆![]() 的直径为9.
的直径为9.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的正切值.
的平面角的正切值.

(1)见解析 (2) ![]()
解析:
(1)证明:∵![]() 垂直于圆
垂直于圆![]() 所在平面,
所在平面,![]() 在圆
在圆![]() 所在平面上,
所在平面上,
∴![]()
![]() .
.
在正方形![]() 中,
中,![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
(2)解法1:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .
.
∴![]() 为圆
为圆![]() 的直径,即
的直径,即![]() .
.
设正方形![]() 的边长为
的边长为![]() ,
,
在![]() △
△![]() 中,
中,![]() ,
,
在![]() △
△![]() 中,
中,![]() ,
,
由![]() ,解得,
,解得,![]() .
.
∴![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,
,

由于![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() .
.
∴![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() △
△![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() .
.
在![]() △
△![]() 中,
中,![]() ,
,
∴![]() .
.
故二面角![]() 的平面角的正切值为
的平面角的正切值为![]() .
.
解法2:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .
.
∴![]() 为圆
为圆![]() 的直径,即
的直径,即![]() .
.
设正方形![]() 的边长为
的边长为![]() ,
,
在![]() △
△![]() 中,
中,![]() ,
,
在![]() △
△![]() 中,
中,![]() ,
,
由![]() ,解得,
,解得,![]() .
.
∴![]() .
.

以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 所在的直线为
所在的直线为![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则 即
即
取![]() ,则
,则![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
设平面![]() 的法向量为
的法向量为![]() ,
,
则 即
即
取![]() ,则
,则![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
∵ ,
,
∴![]() .
.
∴![]() .
.
故二面角![]() 的平面角的正切值为
的平面角的正切值为![]() .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图6,正方形
如图6,正方形 所在平面与圆
所在平面与圆 所在平面相交于
所在平面相交于 ,
, 垂直于圆
垂直于圆 是圆
是圆 、
、 的点,
的点, ,圆
,圆 平面
平面 ;
; 的平面角的正切值.
的平面角的正切值.
 所在平面与圆
所在平面与圆 所在平面相交于
所在平面相交于 ,线段
,线段 垂直于圆
垂直于圆 是圆
是圆 、
、 的点,
的点, ,圆
,圆 平面
平面 ;
;
 所在平面与圆
所在平面与圆 所在平面相交于
所在平面相交于 ,
,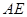 垂直于圆
垂直于圆 是圆
是圆 、
、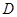 的点,
的点,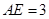 ,圆
,圆 平面
平面 ;
; 的平面角的正切值.
的平面角的正切值.