题目内容
【题目】已知椭圆![]() :
:![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)若动点![]() 为
为![]() 外一点,且
外一点,且![]() 到
到![]() 的两条切线相互垂直,求
的两条切线相互垂直,求![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设![]() 的另一个焦点为
的另一个焦点为![]() ,自直线
,自直线![]() :
:![]() 上任意一点
上任意一点![]() 引(2)所求轨迹
引(2)所求轨迹![]() 的一条切线,切点为
的一条切线,切点为![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)证明见解析
(3)证明见解析
【解析】
(1)根据离心率和焦点坐标可求得![]() 的值,进而得到椭圆的方程;
的值,进而得到椭圆的方程;
(2)设![]() ,切点分别为
,切点分别为![]() ,
,![]() ,对点
,对点![]() 的位置进行讨论,即切线
的位置进行讨论,即切线![]() 的斜率不存在和存在时;当
的斜率不存在和存在时;当![]() 设切线方程为
设切线方程为![]() 代入椭圆的方程得到关于
代入椭圆的方程得到关于![]() 的二次方程,利用直线互相垂直得到
的二次方程,利用直线互相垂直得到![]() 的关系,从而得到点
的关系,从而得到点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设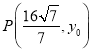 ,将
,将![]() ,
,![]() 都用
都用![]() 进行表示,即可得答案.
进行表示,即可得答案.
(1)设![]() ,
,
由题设,得![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() 的标准方程为
的标准方程为![]() .
.
(2)设![]() ,切点分别为
,切点分别为![]() ,
,![]() ,
,
当![]() 时,设切线方程为
时,设切线方程为![]() ,
,
联立方程,得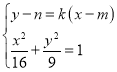 ,
,
消去![]() ,得
,得![]() ,①
,①
关于![]() 的方程①的判别式
的方程①的判别式![]() ,
,
化简,得![]() ,②
,②
关于![]() 的方程②的判别式
的方程②的判别式![]()
![]() ,
,
因为![]() 在椭圆
在椭圆![]() 外,
外,
所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
关于![]() 的方程②有两个实根
的方程②有两个实根![]() ,
,![]() 分别是切线
分别是切线![]() ,
,![]() 的斜率.
的斜率.
因为![]() ,所以
,所以![]() ,即
,即![]() ,化简为
,化简为![]() .
.
当![]() 时,可得
时,可得![]() ,满足
,满足![]() ,
,
所以![]() 的轨迹方程为
的轨迹方程为![]() .
.
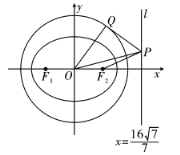
(3)如图,![]() ,设
,设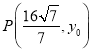 ,
,
![]() ,
,
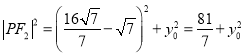 ,
,
所以![]() ,即
,即![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目