题目内容
公比为2的等比数列{an}的各项都为正数,且a2a6=16,则a4=________;a1+a2+a3+…+a10=________.
4 
分析:由题意易得a4=4,进而可得首项,代入求和公式即得答案.
解答:由等比数列的性质可得: =a2a6=16,
=a2a6=16,
又数列各项都为正,故a4=4,
又公比为2,故首项a1=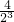 =
= ,
,
由求和公式可得:a1+a2+a3+…+a10
= =
= ,
,
故答案为:4,
点评:本题考查等比数列的通项公式和求和公式,属基础题.

分析:由题意易得a4=4,进而可得首项,代入求和公式即得答案.
解答:由等比数列的性质可得:
 =a2a6=16,
=a2a6=16,又数列各项都为正,故a4=4,
又公比为2,故首项a1=
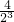 =
= ,
,由求和公式可得:a1+a2+a3+…+a10
=
 =
= ,
,故答案为:4,

点评:本题考查等比数列的通项公式和求和公式,属基础题.

练习册系列答案
相关题目
 如图所示的n×n(n∈N*)的实数数表,满足每一行都是公差为1的等差数列,第一列都是公比为2的等比数列.已知a11=2,则a11+a22+a33+…+ann=
如图所示的n×n(n∈N*)的实数数表,满足每一行都是公差为1的等差数列,第一列都是公比为2的等比数列.已知a11=2,则a11+a22+a33+…+ann= (2012•焦作模拟)在公比为2的等比数列{an}中,a2与a4的等差中项是
(2012•焦作模拟)在公比为2的等比数列{an}中,a2与a4的等差中项是