题目内容
函数 的单调增区间为________.
的单调增区间为________.
[-4,-1]
分析:首先求出函数 的定义域,然后求出定义域内内层函数的增区间,又外层函数是增函数,
的定义域,然后求出定义域内内层函数的增区间,又外层函数是增函数,
所以内层函数在定义域内的增区间即为原函数的增区间.
解答:由-x2-2x+8≥0,得x2+2x-8≤0,解得-4≤x≤2.
所以原函数的定义域为{x|-4≤x≤2}.
令t=-x2-2x+8,其图象是开口向下的抛物线,对称轴方程为 .
.
所以当x∈[-4,-1]时,函数t=-x2-2x+8为增函数,
且函数 为增函数,
为增函数,
所以复合函数 的单调增区间为[-4,-1].
的单调增区间为[-4,-1].
故答案为[-4,-1].
点评:本题考查复合函数的单调性,幂函数函数的单调性,注意复合函数的单调性符合“同增异减”的原则,是中档题.
分析:首先求出函数
 的定义域,然后求出定义域内内层函数的增区间,又外层函数是增函数,
的定义域,然后求出定义域内内层函数的增区间,又外层函数是增函数,所以内层函数在定义域内的增区间即为原函数的增区间.
解答:由-x2-2x+8≥0,得x2+2x-8≤0,解得-4≤x≤2.
所以原函数的定义域为{x|-4≤x≤2}.
令t=-x2-2x+8,其图象是开口向下的抛物线,对称轴方程为
 .
.所以当x∈[-4,-1]时,函数t=-x2-2x+8为增函数,
且函数
 为增函数,
为增函数,所以复合函数
 的单调增区间为[-4,-1].
的单调增区间为[-4,-1].故答案为[-4,-1].
点评:本题考查复合函数的单调性,幂函数函数的单调性,注意复合函数的单调性符合“同增异减”的原则,是中档题.

练习册系列答案
相关题目
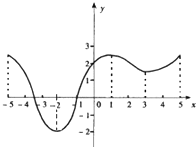 如图是定义在闭区间[-5,5]上的函数y=f(x)图象,该函数的单调增区间为( )
如图是定义在闭区间[-5,5]上的函数y=f(x)图象,该函数的单调增区间为( ) 的单调增区间为(0,+∞),则实数
的单调增区间为(0,+∞),则实数 的取值范围是________.
的取值范围是________. 的单调增区间为_________________。
的单调增区间为_________________。