题目内容
(文)已知等比数列{xn}的公比是不为1的正数,数列{yn}满足 ,当y4=15,y7=9时,数列{yn}的前k项和最大,则k的值为
,当y4=15,y7=9时,数列{yn}的前k项和最大,则k的值为
- A.9
- B.10
- C.11
- D.12(yn=23-2n)
C
分析:先写出两数列的关系,用数列{xn}表示数列{yn},再由等差数列的定义证明数列{yn}为等差数列,最后写出数列{yn}的通项公式,分析其前n项和的最大值即可
解答:依题意,yn=2logaxn,由yn-yn-1=2log(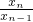 )=2q (q为等比数列{xn}的公比)
)=2q (q为等比数列{xn}的公比)
∴数列{yn}是等差数列,又∵y4=15,y7=9
∴yn=23-2n,由yn≥0,得n≤11,即y11>0,y12<0
∴数列{yn}的前11项和最大
故选C
点评:本题考查了等差数列和等比数列的定义,及等差数列的前n项和的性质,解题时要体会等差数列和等比数列是怎样相互转化的
分析:先写出两数列的关系,用数列{xn}表示数列{yn},再由等差数列的定义证明数列{yn}为等差数列,最后写出数列{yn}的通项公式,分析其前n项和的最大值即可
解答:依题意,yn=2logaxn,由yn-yn-1=2log(
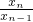 )=2q (q为等比数列{xn}的公比)
)=2q (q为等比数列{xn}的公比)∴数列{yn}是等差数列,又∵y4=15,y7=9
∴yn=23-2n,由yn≥0,得n≤11,即y11>0,y12<0
∴数列{yn}的前11项和最大
故选C
点评:本题考查了等差数列和等比数列的定义,及等差数列的前n项和的性质,解题时要体会等差数列和等比数列是怎样相互转化的

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,定义数列
,定义数列 为数列
为数列 =2,
=2,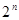 ,则数列
,则数列 =
=  ,
, ,则
,则 =
=