题目内容
已知函数
(1)f(x)为定义域上的单调函数,求实数m的取值范围;
(2)当m=﹣1时,求函数f(x)的最大值;
(3)当m=1时,且1≧a>b≧0,证明: .
.

(1)f(x)为定义域上的单调函数,求实数m的取值范围;
(2)当m=﹣1时,求函数f(x)的最大值;
(3)当m=1时,且1≧a>b≧0,证明:
 .
.解:(1)函数的定义域为(﹣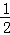 ,+∞)
,+∞)
求导函数可得f′(x)=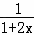 +m.
+m.
∵x>﹣ ,
,
∴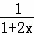 >0,
>0,
∴不存在实数m,使f′(x)=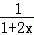 +m<0对x>﹣
+m<0对x>﹣ 恒成立,
恒成立,
由f′(x)=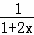 +m≧0对x>﹣
+m≧0对x>﹣ 恒成立得,m≧
恒成立得,m≧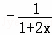
对x>﹣ 恒成立
恒成立
而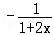 <0,故m≧0
<0,故m≧0
经检验,当m≧0时,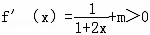 对x>﹣
对x>﹣ 恒成立
恒成立
∴当m≧0时,f(x)为定义域上的单调递增函数。
(2)当m=-1时,由f′(x)=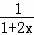 ﹣1=0,可得x=0
﹣1=0,可得x=0
当x∈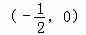 时,f′(x)>0;
时,f′(x)>0;
当x∈(0,+∞)时,f′(x)<0
∴函数f(x)在x=0时取得最大值,最大值为f(0)=0
(3)证明:当m=1时,令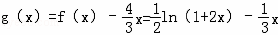
∴ 在[0,1]上总有g′(x)≧0,
在[0,1]上总有g′(x)≧0,
即g(x)在[0,1]上递增
∴当1≧a>b≧0时,g(a)>g(b),
即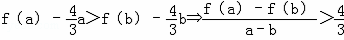 .
.
令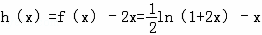 ,
,
由(2)知它在[0,1]上递减,
∴h(a)<h(b)
即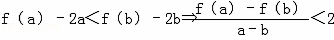 ,
,
综上所述,当m=1,且1≧a>b≧0时,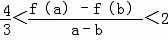 。
。
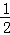 ,+∞)
,+∞)求导函数可得f′(x)=
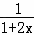 +m.
+m.∵x>﹣
 ,
,∴
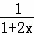 >0,
>0,∴不存在实数m,使f′(x)=
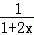 +m<0对x>﹣
+m<0对x>﹣ 恒成立,
恒成立,由f′(x)=
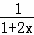 +m≧0对x>﹣
+m≧0对x>﹣ 恒成立得,m≧
恒成立得,m≧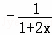
对x>﹣
 恒成立
恒成立而
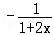 <0,故m≧0
<0,故m≧0经检验,当m≧0时,
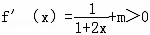 对x>﹣
对x>﹣ 恒成立
恒成立∴当m≧0时,f(x)为定义域上的单调递增函数。
(2)当m=-1时,由f′(x)=
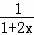 ﹣1=0,可得x=0
﹣1=0,可得x=0当x∈
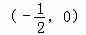 时,f′(x)>0;
时,f′(x)>0;当x∈(0,+∞)时,f′(x)<0
∴函数f(x)在x=0时取得最大值,最大值为f(0)=0
(3)证明:当m=1时,令
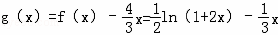
∴
 在[0,1]上总有g′(x)≧0,
在[0,1]上总有g′(x)≧0,即g(x)在[0,1]上递增
∴当1≧a>b≧0时,g(a)>g(b),
即
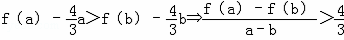 .
. 令
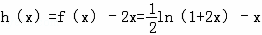 ,
,由(2)知它在[0,1]上递减,
∴h(a)<h(b)
即
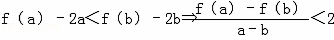 ,
,综上所述,当m=1,且1≧a>b≧0时,
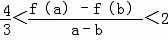 。
。
练习册系列答案
相关题目

 .
.
 .
.
 .
.
 .
.