题目内容
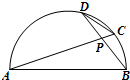（2012•深圳二模）（几何证明选讲选做题）如图，AB是半圆的直径，弦AC和弦BD相交于点P，且AB=3DC，则sin∠APD=2
| ||
| 3 |
2
| ||
| 3 |
分析：由圆周角定理，我们可得∠A=∠D，∠B=∠C，结合相似三角形判断定理可得△ABP∽△DCP，进而由相似三角形的性质我们可得DP：AP=DC：AB=
，即cos∠APD=
，再由同角三角函数关系，即可得到答案．
| 1 |
| 3 |
| 1 |
| 3 |
解答：解：由圆周角定理，可得：
在△ABP和△DCP中
∠A=∠D，∠B=∠C
∴△ABP∽△DCP
所以DP：AP=DC：AB=
，连接DA
因为AB是圆O直径
所以∠ADP=90°
∴cos∠APD=
，
∴sin∠APD=
=
．
故答案为：
．
在△ABP和△DCP中
∠A=∠D，∠B=∠C
∴△ABP∽△DCP
所以DP：AP=DC：AB=
| 1 |
| 3 |
因为AB是圆O直径
所以∠ADP=90°
∴cos∠APD=
| 1 |
| 3 |
∴sin∠APD=
| 1-cos2∠APD |
2
| ||
| 3 |
故答案为：
2
| ||
| 3 |
点评：本题考查的知识点是圆周角定理，相似三角形的判定与性质，同角三角函数关系，其中利用三角形相似的性质，得到cos∠APD=
，是解答本题的关键．
| 1 |
| 3 |
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
