题目内容
下面四个函数:①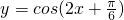 ;②
;②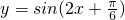 ;③
;③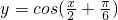 ;④
;④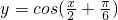 中,同时具有“最小正周期是
中,同时具有“最小正周期是 对称”两个性质的函数序号是________.
对称”两个性质的函数序号是________.
①
分析:利用已知的周期为π,利用周期公式求出ω的值,对四个函数作出筛选,再利用图象关于点( ,0)对称对剩下的函数作出判断,即可得到同时满足两性质的函数.
,0)对称对剩下的函数作出判断,即可得到同时满足两性质的函数.
解答:函数最小正周期是π,所以 ,由选项可知:ω>0,
,由选项可知:ω>0,
所以ω=2,排除③④;
图象关于点( ,0)对称,所以x=
,0)对称,所以x= 时,函数值为0,
时,函数值为0,
此时 =
= ,
,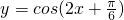 =cos
=cos =0,选项①正确;
=0,选项①正确;
而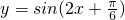 =sin
=sin =1≠0,选项②错误,
=1≠0,选项②错误,
则同时满足两个性质的函数序号是①.
故答案为:①
点评:本题考查了三角函数的周期性及其求法,以及正弦、余弦函数的对称性,锻炼了学生的推理能力,以及计算能力.
分析:利用已知的周期为π,利用周期公式求出ω的值,对四个函数作出筛选,再利用图象关于点(
 ,0)对称对剩下的函数作出判断,即可得到同时满足两性质的函数.
,0)对称对剩下的函数作出判断,即可得到同时满足两性质的函数.解答:函数最小正周期是π,所以
 ,由选项可知:ω>0,
,由选项可知:ω>0,所以ω=2,排除③④;
图象关于点(
 ,0)对称,所以x=
,0)对称,所以x= 时,函数值为0,
时,函数值为0,此时
 =
= ,
,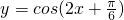 =cos
=cos =0,选项①正确;
=0,选项①正确;而
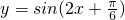 =sin
=sin =1≠0,选项②错误,
=1≠0,选项②错误,则同时满足两个性质的函数序号是①.
故答案为:①
点评:本题考查了三角函数的周期性及其求法,以及正弦、余弦函数的对称性,锻炼了学生的推理能力,以及计算能力.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目